数学分布(泊松分布二项分布正态分布均匀分布指数分布)生存分析贝叶斯概率公式全概率公式

数学期望：随机变量最基本的数学特征之一。它反映随机变量平均取值的大小。又称期望或均值。它是简单算术平均的一种推广。例如某城市有10万个家庭，没有孩子的家庭有1000个，有一个孩子的家庭有9万个，有两个孩子的家庭有6000个，有3个孩子的家庭有3000个，则此城市中任一个家庭中孩子的数目是一个随机变量，记为X，它可取值0，1，2，3，其中取0的概率为0.01，取1的概率为0.9，取2的概率为0.06，取3的概率为0.03，它的数学期望为0×0.01＋1×0.9＋2×0.06＋3×0.03等于1.11，即此城市一个家庭平均有小孩1.11个，用数学式子表示为：E(X)=1.11。

也就是说，我们用数学的方法分析了这个概率性的问题，对于每一个家庭，最有可能它家的孩子为1.11个。

可以简单的理解为求一个概率性事件的平均状况。

各种数学分布的方差是：

1、一个完全符合分布的样本

2、这个样本的方差

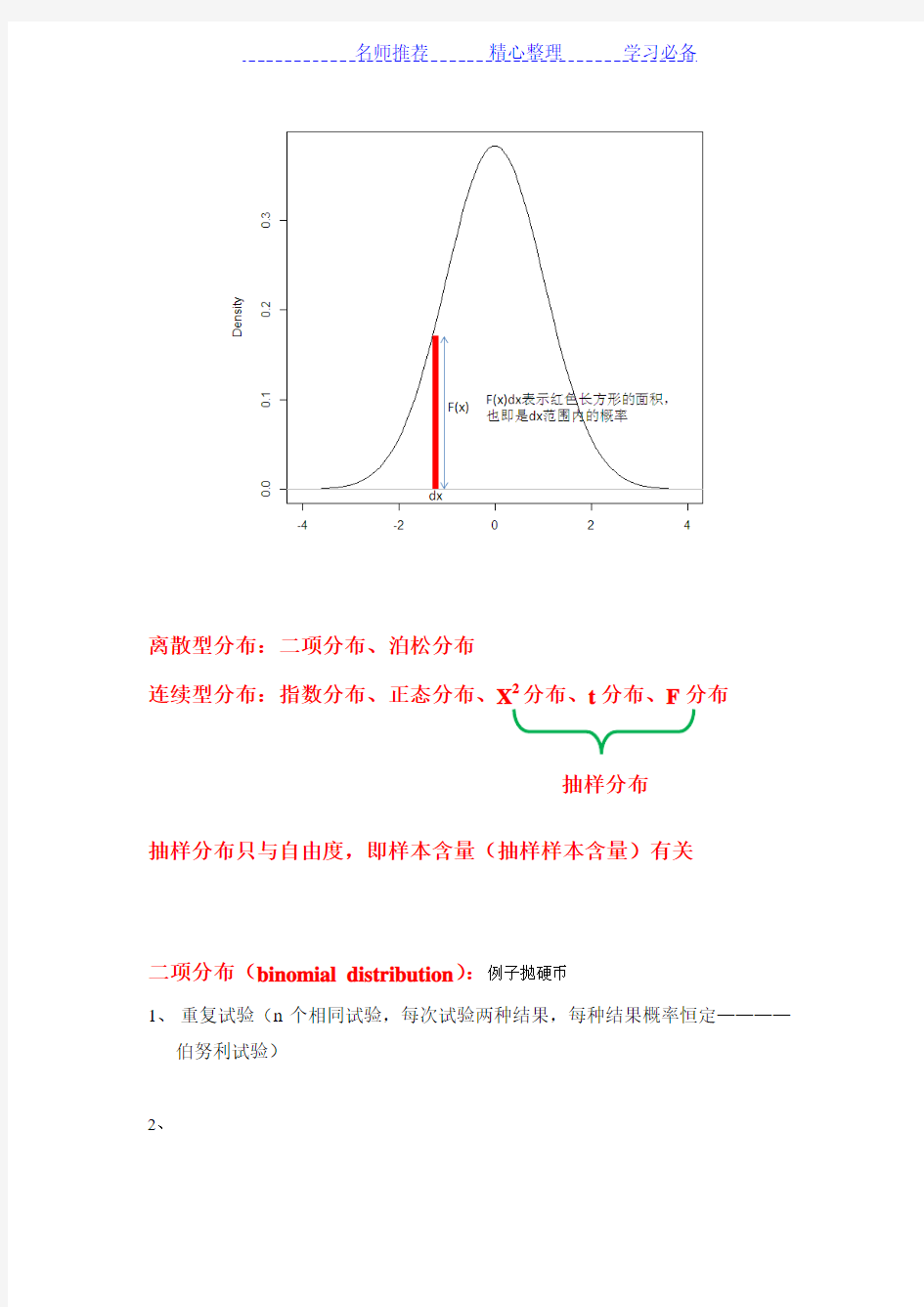
概率密度的概念是：某种事物发生的概率占总概率(1)的比例,越大就说明密度越大。比如某地某次考试的成绩近似服从均值为80的正态分布，即平均分是80分，由正态分布的图形知x=80时的函数值最大，即随机变量在80附近取值最密集，也即考试成绩在80分左右的人最多。

下图为概率密度函数图(F(x)应为f(x)，表示概率密度)：

离散型分布：二项分布、泊松分布

连续型分布：指数分布、正态分布、X 2分布、t 分布、F 分布

抽样分布只与自由度，即样本含量（抽样样本含量）有关

二项分布（binomial distribution ）：例子抛硬币

1、 重复试验（n 个相同试验，每次试验两种结果，每种结果概率恒定————伯努利试验）

2、

抽样分布

3、P(X=0), P(X=1), P(X=3), ……….所有可能的概率共同组成了一个分布，即二

项分布

泊松分布（possion distribution）：

1、一个单位内（时间、面积、空间）某稀有事件

2、此事件发生K次的概率

3、P(X=0), P(X=1), P(X=3), ……….所有可能的概率共同组成了一个分布，即泊

松分布

二项分布与泊松分布的关系：

二项分布在事件发生概率很小，重复次数n很大的情况下，其分布近似泊松分布

均匀分布(uniform distribution)：

分为连续型均匀分布和离散型均匀分布

离散型均匀分布：

1、n种可能的结果

2、每个可能的概率相等(1/n)

连续型均匀分布：

1、可能的结果是连续的

2、每个可能的概率相等()

连续型均匀分布概率密度函数如下图：

指数分布（exponential distribution）：

用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

指数分布常用于各种“寿命”分布的近似。

1、连续型分布，每个点的概率：

2、无记忆性。已经使用了s小时的元件，它能再使用t小时的概率，与一个从未使用过的元件使用t小时的概率相同。即它对已经使用过的s小时没有记忆。

指数分布的概率密度函数如下图：

正态分布（normal distribution）：

又称高斯分布。

1、描述一个群体的某个指标。

2、这个指标是连续的。

3、每个特定指标在整个群体中都有一个概率（）。

4、所有指标概率共同组成了一个分布，这个分布就是正态分布。正态分布的概率密度函数如下图：

中心极限定理：

不论总体的分布形式如何（正态或非正态），只要样本（抽样样本）含量n足够大时，样本均数的分布就近似正态分布，且均数与总体均数相等，标准差为（总体标准差）/（n的开方）。

中心极限定理使得t分布、F分布和X2分布在抽样样本含量很大时不需要对总体样本是否正态有要求。

t分布（student t distribution）:

1、t分布是以0为中心的一簇曲线，每个自由度决定一个曲线

2、自由度是一个抽样小样本中的具体观测值的个数（抽样样本含量）-1

3、总体样本呈正态分布（抽样样本含量较小时，要求总体样本呈正态分布，如果抽样样

本含量很大（eg. n >= 100），由中心极限定理可知抽样样本均数也近似正态分布，因而“差值”的概率也呈正态分布，而t分布的每一条曲线实际上都是正态分布曲线）

4、从一个总体样本中抽取很多个小样本———抽样

5、每个小样本都有一个均值

6、每个小样本的均值与总体样本均值有一个差值，这个差值用t估计

7、可能有多个小样本的差值估计都是t，t出现的次数占所有小样本的比例可以用一个概率衡量

8、所有t值的概率组成一个分布，就是t分布的一个曲线

9、另外做一个抽样，每个小样本包含的观测值不同，则形成t分布的另外一个

曲线

10、自由度越大，则曲线越接近于标准正态分布

11、t分布只与自由度相关

t分布的概率密度函数如下图（v为自由度）：

X2分布（chi square distribution）：

1、X2分布也是一簇曲线，每个自由度决定一个曲线

2、自由度是一个抽样小样本中的具体观测值的个数（抽样样本含量）-1

2、总体样本呈正态分布（抽样样本含量（n）较小时，要求总体样本呈正态分布）

3、从总体样本中抽取n个观测值：z1，z2，z3……———抽样

4、将它们平方后求和，这个和用一个新变量表示，即X2

5、重复抽样并获得多个X2：X12，X22，X32，X42………

6、可能有多次抽样的X2值相同，同一个X2值的抽样次数占总次数的比例可以用一个概率表示

7、所有的概率值共同组成一个分布，就是X2分布的一条曲线

8、另外做一次，只要从总体中选取观测值数目n不同，得到的就是另外一条曲线

10、自由度越大，则曲线越接近于标准正态分布

11、X2分布只与自由度相关

X2分布的概率密度函数如下图（n在这里为自由度）：

F分布（F-distribution）：

1、F分布也是一簇曲线，每对自由度决定一个曲线

2、自由度是一个抽样小样本中的具体观测值的个数（抽样样本含量）-1

2、两总体样本方差比的分布

3、总体样本呈正态分布（抽样样本含量（n）较小时，要求总体样本呈正态分布）

4、从总体样本中抽取两个样本，两个样中的观测值数目可相同也可不同，分别

记为n1和n2

5、分别计算出X2：X1，X2

6、构建一个新变量F：

7、重复抽取样本，计算多个F值：F1，F2，F3……..

8、可能有多次抽样的F值相同，同一个F值的抽样次数占总次数的比例可以用一个概率表示

9、所有的概率值共同组成一个分布，就是F分布的一条曲线

10、另外做一次，只要从总体中选取观测值数目n不同，得到的就是另外一条曲线

10、两个自由度越大，则曲线越接近于标准正态分布

11、F分布只与自由度相关

F分布的概率密度函数如下图（m，n在这里为自由度）：

【在推估总体平均值时，基于样本平均数的抽样分布】——t分布【在用样本方差来推估总体方差时，必须知道样本方差的抽样分布】—X2分布【比较两个总体的方差是否相等时，必须知道样本方差的联合抽样分布】—F 分布

生存分析（survival analysis）：

1、多种影响慢性疾病的因素（不同手术方法、不同药物………）

2、随访一群患者

3、一段时间后统计生存和死亡

3、最终给出的结果是一个评价各种因素对生存时间的影响（生存时间、生存率有无差异）

贝叶斯公式（bayes formula）：

1、描述两个条件概率之间的关系———P(Bi|A)与P(A|Bi)，A为事件，Bi 为一个划分

2、P(Bi|A)=P(A|Bi)*P(Bi)/P(A) 或者

3、看图理解

全概率公式（full probability formula）：

1、描述一个特定事件的概率与条件概率间的关系

2、P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn)

3、看图理解

§11.4 条件概率、二项分布

§11.4 条件概率、二项分布 【复习目标】 独立重复试验、二项分布的理解及应用二项分布模型解决一些简单的实际问题。 【知识梳理】 1． 条件概率 叫作B 发生时A 发生的条件概率，用符号P (A |B )来表示，其公式为 2． 相互独立事件 (1)一般地，对于两个事件A ，B ，如果有 ，则称A 、B 相互独立． (2)如果A 、B 相互独立，则 也相互独立． (3)如果A 1，A 2，…，A n 相互独立，则有： ． 3． 二项分布 进行n 次试验，如果满足以下条件： (1)每次试验只有两个相互对立的结果： ； (2)每次试验“成功”的概率均为p ，“失败”的概率均为 ； (3)各次试验是 ． 用X 表示这n 次试验成功的次数，则P (X ＝k )＝ (k ＝0,1,2，…，n ) 若一个随机变量X 的分布列如上所述，称X 服从参数为n ，p 的二项分布，简记为X ～B (n ，p )． 【复习自测】 1． 把一枚硬币连续抛两次，记“第一次出现正面”为事件A ，“第二次出现正面”为事件B ，则P (B |A )等于 ( ) A.12 B.14 C.16 D.18 2． 某一批花生种子，如果每粒发芽的概率都为4 5 ，那么播下4粒种子恰有2粒发芽的概率是 ( ) A.16 625 B.96 625 C.192625 D.256625 3． 某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋 级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率为________． 4．某公司是否对某一项目投资，由甲、乙、丙三位决策人投票决定，他们三人都有“同意”、“中立”、“反 对”三类票各一张，投票时，每人必须且只能投一张票，每人投三类票中的任何一类票的概率都为1 3，他们的投 票相互没有影响，规定：若投票结果中至少有两张“同意”票，则决定对该项目投资；否则，放弃对该项目的投资． (1)求该公司决定对该项目投资的概率； (2)求该公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率． 【合作探究】 例1 在100件产品中有95件合格品，5件不合格品．现从中不放回地取两次，每次任取一件，则在第一次取 到不合格品后，第二次再取到不合格品的概率为________． 例2 甲、乙两人轮流投篮，每人每次投一球．约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3 次时投篮结束．设甲每次投篮投中的概率为13，乙每次投篮投中的概率为1 2，且各次投篮互不影响． (1)求乙获胜的概率；(2)求投篮结束时乙只投了2个球的概率．

全概率公式和贝叶斯公式

单位代码：005 分类号：o1 西安创新学院本科毕业论文设计 题目：全概率公式和贝叶斯公式 专业名称：数学与应用数学 学生姓名：行一舟 学生学号：0703044138 指导教师：程值军 毕业时间：二0一一年六月

全概率公式和贝叶斯公式 摘要:对全概率公式和贝叶斯公式,探讨了寻找完备事件组的两个常用方法,和一些实际的应用.全概率公式是概率论中的一个重要的公式,它提供了计算复杂事件概率的一条有效的途径,使一个复杂事件的概率计算问题化繁就简.而贝叶斯公式则是在乘法公式和全概率公式的基础上得到的一个著名的公式. 关键词:全概率公式;贝叶斯公式;完备事件组

The Full Probability Formula and Bayes Formula Abstract：To the full probability formula and bayes formula for complete,discusses the two commonly used methods of events,and some practical applications.Full probability formula is one of the important full probability formula of calculation,it provides an effective complex events of the way the full probability of a complex events,full probability calculation problem change numerous will Jane.And the bayes formula is in full probability formula multiplication formula and the basis of a famous formula obtained. Key words：Full probability formula;Bayes formula;Complete event group;

贝叶斯决策模型与实例分析报告

贝叶斯决策模型及实例分析 一、贝叶斯决策的概念 贝叶斯决策，是先利用科学试验修正自然状态发生的概率，在采用期望效用最大等准则来确定最优方案的决策方法。 风险型决策是根据历史资料或主观判断所确定的各种自然状态概率（称为先验概率），然后采用期望效用最大等准则来确定最优决策方案。这种决策方法具有较大的风险，因为根据历史资料或主观判断所确定的各种自然状态概率没有经过试验验证。为了降低决策风险，可通过科学试验（如市场调查、统计分析等）等方法获得更多关于自然状态发生概率的信息，以进一步确定或修正自然状态发生的概率；然后在利用期望效用最大等准则来确定最优决策方案，这种先利用科学试验修正自然状态发生的概率，在采用期望效用最大等准则来确定最优方案的决策方法称为贝叶斯决策方法。 二、贝叶斯决策模型的定义 贝叶斯决策应具有如下容 贝叶斯决策模型中的组成部分： ) ( ,θ θP S A a及 ∈ ∈。概率分布S P∈ θ θ) (表示决策 者在观察试验结果前对自然θ发生可能的估计。这一概率称为先验分布。 一个可能的试验集合E，E e∈，无情报试验e0通常包括在集合E之。 一个试验结果Z取决于试验e的选择以Z0表示的结果只能是无情报试验e0的结果。 概率分布P(Z/e,θ)，Z z∈表示在自然状态θ的条件下，进行e试验后发生z结果

的概率。这一概率分布称为似然分布。 c 以及定义在后果集合C的效用函数u(e,Z,a,θ)。 一个可能的后果集合C，C 每一后果c=c(e,z,a,θ)取决于e,z,a和θ。.故用u(c)形成一个复合函数u{(e,z,a,θ)}，并可写成u(e,z,a,θ)。 三、贝叶斯决策的常用方法 3.1层次分析法(AHP) 在社会、经济和科学管理领域中，人们所面临的常常是由相互关联，相互制约的众多因素组成的复杂问题时，需要把所研究的问题层次化。所谓层次化就是根据所研究问题的性质和要达到的目标，将问题分解为不同的组成因素，并按照各因素之间的相互关联影响和隶属关系将所有因素按若干层次聚集组合，形成一个多层次的分析结构模型。 3.1.1层次分析模型 最高层：表示解决问题的目的，即层次分析要达到的目标。 中间层：表示为实现目标所涉及的因素，准则和策略等中间层可分为若干子层，如准则层，约束层和策略层等。 最低层：表示事项目标而供选择的各种措施，方案和政策等。 3.1.2层次分析法的基本步骤 (l) 建立层次结构模型 在深入分析研究的问题后，将问题中所包括的因素分为不同层次，如目标层、指标层和措施层等并画出层次结构图表示层次的递阶结构和相邻两层因素的从属关系。 (2) 构造判断矩阵 判断矩阵元素的值表示人们对各因素关于目标的相对重要性的认识。在相邻的两个层次中，高层次为目标，低层次为因素。 (3) 层次单排序及其一致性检验 判断矩阵的特征向量W经过归一化后即为各因素关于目标的相对重要性的排序权值。利用判断矩阵的最大特征根，可求CI和CR值，当CR<0.1时，认为层次单排序的结果有满意的一致性；否则，需要调整判断矩阵的各元素的取值。 (4) 层次总排序 计算某一层次各因素相对上一层次所有因素的相对重要性的排序权值称为层次总排序。由于层次总排序过程是从最高层到最低层逐层进行的，而最高层是总目标，所以，层次总排序也是计算某一层次各因素相对最高层（总目标）的相对重要性的排序权值。 设上一层次A包含m个因素A1,A2,…,A m其层次总排序的权值分别为a1,a2,…,a m；下一层次B包含n个因素B1,B2,…,B n，它们对于因素A j(j=1,2,…,m)的层次单排序权值分别为：b1j,b2j,…,b nj（当B k与A j无联系时，b kj=0），则B层次总排序权值可按下表计算。 层次总排序权值计算表

【方法指导】《条件概率与独立事件、二项分布》学习指导1

《条件概率与独立事件、二项分布》学习指导 一．重、难点释疑及实例剖 1．重、难点释疑 （1）了解条件概率，并掌握条件概率的公式P （A|B ）＝ ) ()(B P AB P ，并理解条件概率的 性质：任何事件的条件概率都在0和1之间，即0≤P （A|B ）≤1； （2）了解两个事件相互独立的概念，区别事件的“互斥”与“相互独立”是两个不同的概念；掌握公式P （AB ）=P （A ）P （B ）使用的前提条件：事件A 、B 为相互独立事件；理解1－P （A ）P （B ）表示两个相互独立事件A 、B 至少有一个不发生的概率． （3）理解二项分布：X ～B （n ，p ），掌握二项分布的概率计算公式：P （X=k ）=k n C （1－p ）n －k p k ，以及对应的概率分布列，掌握二项分布的常见实例：反复抛掷一枚均匀硬币、已知次品率的抽样、有放回的抽样、射手射击目标命中率已知的若干次射击等，并能解决一些简单的实际问题； （4）独立事件的概率、二项分布是高考考查的重点内容，对这部分知识的考查通常与其他知识结合在一起有一定的综合性． 2．实例剖析 （1）条件概率问题 例1．在10个各不相同的球中有6个红球和4个白球，不放回地依次摸出2个球，在第一次摸出红球的条件下，第二次也摸到红球的概率为（ ） A ． 5 3 B ．5 2 C ．10 1 D ．9 5 分析：从题设可知，这是一个条件概率问题，可设出要求的事件A 、B ，由条件概率公式进行求解． 解析：方法一：设事件A ＝“第二次摸到红球”，事件B ＝“第一次摸到红球”， 则事件A|B 表示“在第一次摸出红球的条件下，第二次也摸到红球”， 由题意知，B 发生后，袋中还有9个球，其中5个红球4个白球，A 发生的概率为9 5， 即P （A|B ）＝ 9 5． 方法二：设事件A ＝“第二次摸到红球”，事件B ＝“第一次摸到红球”， 则有P （B ）＝106 ＝53 ，P （AB ）＝ 210 26A A = 31 ，那么有P （A|B ）＝ ) () (B P AB P ＝5 331 ＝95 ． 点评：此题为一典型的求解条件概率问题，解决中用了不同的思路，既可以根据条件概率的含义解决，也可以由条件概率公式求解，无论哪种方法，必须准确地找对事件A 、B 、 A|B 、AB ，并熟练地求出其概率． （2）独立事件问题 例2．某集团公司招聘员工，指定三门考试课程，有两种考试方案． 方案一：考试三门课程，至少有两门及格为考试通过； 方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

全概率公式与贝叶斯公式解题归纳

全概率公式与贝叶斯公式解题归纳 来源：文都教育 在数学一、数学三的概率论与数理统计部分，需要用到全概率公式及其贝叶斯公式来解题. 这类题目首先要区分清楚是“由因导果”，还是“由果索因”，因为全概率公式是计算由若干“原因”引起的复杂事件概率的公式，而贝叶斯公式是用来计算复杂事件已发生的条件下，某一“原因”发生的条件概率. 它们的定义如下： 全概率公式：设n B B B ,,,21 为样本空间Ω的一个划分，如果()0,i P B > 1,2,,i n =L ，则对任一事件A 有 )|()()(1 i n i i B A P B P A P ∑==. 贝叶斯公式 ：设n ,B ,,B B 21 是样本空间Ω的一个划分，则 .,,2,1,)|()() |()()|(1n i B A P B P B A P B P A B P n j j j i i i ==∑= 例1 从数字1, 2, 3, 4中任取一个数，记为X ，再从1，…，X 中任取一个数，记为Y ，则(2)P Y == . 解 由离散型随机变量的概率分布有： (1)(2)(3)(4)14P X P X P X P X ========. 由题意，得 (21)0,(22)12,P Y X P Y X ====== (23)13,(24)14P Y X P Y X ======,则根据全概率公式得到

(2)(1)(21)(2)(22)P Y P X P Y X P X P Y X =====+=== (3)(23)(4)(24)P X P Y X P X P Y X +===+=== 111113(0).423448 =?+++= 例2 12件产品中有4件次品，在先取1件的情况下，任取2件产品皆为正品，求先取1件为次品的概率. 解 令A={先取的1件为次品}，则,A A 为完备事件组，12(),(),33 P A P A = =令B={后取的2件皆为正品}，则2821128(),55C P B A C ==2721121(),55C P B A C == 由贝叶斯公式得 128()()()2355().128221()()()()()5 355355 P A P B A P AB P A B P B P A P B A P A P B A ?====+?+? 若随机试验可以看成分两个阶段进行，且第一阶段的各试验结果具体结果怎样未知，那么：（1）如果要求的是第二阶段某一个结果发生的概率，则用全概率公式；（2）如果第二个阶段的某一个结果是已知的，要求的是此结果为第一阶段某一个结果所引起的概率，一般用贝叶斯公式，类似于求条件概率. 熟记这个特征，在遇到相关的题目时，可以准确地选择方法进行计算，保证解题的正确高效.

层次贝叶斯模型-空间分析

1.1 层次贝叶斯模型 经典的推断分析模型、空间回归模型、空间面板模型有一个共同的特点：这些模型的求解完全依赖所采集的样本信息。然而，在业务实践中，在收集样本之前，研究者往往会对研究对象的变化或分布规律有一定的认识。这些认识或是来自长期积累的经验，也可能来自合理的假设。由于这些认识没有经过样本的检验，所以我们可以称之为先验知识。比如我们要研究某地某疾病月发病人数的概率分布。即使没有进行统计调查，我们根据一些定理和合理假设，也可以知道发病数服从泊松分布。甚至根据医院日常接诊的经验，可以推算出发病人数大概在哪个区间。这种情况下，对于发病人数分布形态和大致区间的认识，属于先验知识。先验知识对我们探索研究对象的变化规律会有很大的帮助。而经典的推断分析模型、空间回归模型、空间面板模型都没有利用先验知识，导致了信息利用的不充分。而本节所要谈到的层次贝叶斯模型，会结合先验知识和样本信息，对数据进行推断分析。由于层次贝叶斯模型能有效利用先验知识和样本信息，因此可以提高推断的准确度或降低抽样的成本。 （1）贝叶斯统计原理简介 在介绍层次贝叶斯模型之前，有必要首先简单阐述一下贝叶斯统计的基本原理。贝叶斯统计的基础是贝叶斯定理： (|)() (|)()P B A P A P A B P B = （1） 其中: ()P A 是事件A 的先验概率（例如，某专家通过经验或之前的研究得出乙肝发病率为10%，这就是一个先验概率），()P B 是事件B 发生的概率，且()0P B ≠，(|)P A B 是给出事件B 后事件A 的后验概率。(|)/()P B A P B 是事件A 发生对事件B 的支持程度，即似然函数。对(|)/()P B A P B 可以有如下的理解：设(|)/()P B A P B n =，则在事件A 发生的条件下，事件B 发生的概率是不知A 是否发生的条件下的n 倍。 使用贝叶斯方法的一个重要目的，就在于得出随机变量的概率分布及各因素对分布的影响。要实现这一目的，首先按如下公式进行参数反演： (|)(|)()f D Cf D f θθθ= （2）

二项分布

二项分布 科技名词定义 中文名称：二项分布 英文名称：binomial distribution 定义：描述随机现象的一种常用概率分布形式，因与二项式展开式相同而得名。 所属学科：大气科学（一级学科）；气候学（二级学科） 本内容由全国科学技术名词审定委员会审定公布 百科名片 二项分布 二项分布即重复n次的伯努里试验。在每次试验中只有两种可能的结果,而且是互相对立的，是独立的,与其它各次试验结果无关，结果事件发生的概率在整个系列试验中保持不变,则这一系列试验称为伯努力试验。 目录 概念 医学定义 二项分布的应用条件 二项分布的性质 与两点分布区别 编辑本段概念 二项分布（Binomial Distribution），即重复n次的伯努力试验（Bernoulli Experiment）, 用ξ表示随机试验的结果. 如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重

复试验中发生K次的概率是 P(ξ=K)=Cn(k)P(k)q(n-k) 注意!:第二个等号后面的括号里的是上标，表示的是方幂。 那么就说这个属于二项分布.. 其中P称为成功概率。 记作ξ~B(n,p) 期望:Eξ=np 方差:Dξ=npq 如果 1.在每次试验中只有两种可能的结果,而且是互相对立的; 2.每次实验是独立的,与其它各次试验结果无关; 3.结果事件发生的概率在整个系列试验中保持不变,则这一系列试验称为伯努力试验. 在这试验中,事件发生的次数为一随机事件,它服从二次分布.二项分布可 二项分布 以用于可靠性试验.可靠性试验常常是投入n个相同的式样进行试验T小时,而只允许k个式样失败,应用二项分布可以得到通过试验的概率. 若某事件概率为p，现重复试验n次，该事件发生k次的概率 为:P=C(k,n)×p^k×(1-p)^(n-k).C(k,n)表示组合数，即从n个事物中拿出k个的方法数. 编辑本段医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。 考虑只有两种可能结果的随机试验，当成功的概率（π）是恒定的

条件概率与独立事件、二项分布练习题及答案

条件概率与独立事件、二项分布 1．(2012·广东汕头模拟)已知某射击运动员，每次击中目标的概率都是，则该射击运动员射击4次至少击中3次的概率为( ) A ． B ． 2 C ． D ． 2．(2011·广东高考)甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军．若两队胜每局的概率相同，则甲队获得冠军的概率为( ) 3．(2011·湖北高考)如图，用K 、A 1、A 2三类不同的元件连接成一个系统．当K 正常工作且A 1、A 2至少有一个正常工作时，系统正常工作．已知K 、A 1、A 2正常工作的概率依次为、、，则系统正常工作的概率为( ) A ． B ． C ． D ． 4．(2011·辽宁高考)从1,2,3,4,5中任取2个不同的数，事件A ＝“取到的2个数之和为偶数”，事件B ＝“取到的2个数均为偶数”，则P (B |A )＝( ) 5．(2012·山西模拟)抛掷一枚硬币，出现正反的概率都是12，构造数列{a n }，使得a n ＝ ? ???? 1 第n 次抛掷时出现正面，－1 第n 次抛掷时出现反面， 记S n ＝a 1＋a 2＋…＋a n (n ∈N *)，则S 4＝2的概率为( ) 6．高三毕业时，甲、乙、丙等五位同学站成一排合影留念，已知甲、乙二人相邻，则甲、丙相邻的概率是( ) 7．某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为16 25，则该队员每次罚球的命中率为________． 8．某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于________． 9．有一批种子的发芽率为，出芽后的幼苗成活率为，在这批种子中，随机抽取一粒，则这粒种子能成长为幼苗的概率为________．

最新全概率公式和贝叶斯公式练习题

1.设某工厂有两个车间生产同型号家用电器，第一车间的次品率为0.15，第二车间的次品率为0.12，两个车间的成品都混合堆放在一个仓库，假设第1,2车间生产的成品比例为2:3，今有一客户从成品仓库中随机提一台产品，求该产品合格的概率。 解：设B={从仓库中随机提出的一台是合格品} A i ={提出的一台是第i 车间生产的}，i=1,2 则有分解B=A 1B ∪A 2B 由题意P(A1)=2/5,P(A2)=3/5,P(B|A1)=0.85,P(B|A2)=0.88 由全概率公式P(B)= P(A 1) P(B|A 1)+ P(A 2) P(B|A 2)=0.4*0.85+0.6*0.88=0.868. 2. 盒中有a 个红球，b 个黑球，今随机地从中取出一个，观察其颜色后放回，并加上同色球c 个，再从盒中第二次抽取一球，求第二次抽出的是黑球的概率。 解：设A={第一次抽出的是黑球}，B={第二次抽出的是黑球}，则B AB AB =+， 由全概率公式()()()()()P B P A P B A P A P B A =+， 由题意(),(|),(),(|)b b c a b P A P B A P A P B A a b a b c a b a b c +====++++++ 所以()()()()()()b b c ab b P B a b a b c a b a b c a b +=+=+++++++ 3. 设某公路上经过的货车与客车的数量之比为2:1，货车中途停车修理的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，求该汽车是货车的概率。 解：设B={中途停车修理}，A1={经过的是货车}，A2={经过的是客车}，则B=A 1B ∪A 2B ，由贝叶斯公式有 111112220.02()()3()0.80.21()()()()0.020.0133P A P B A P A B P A P B A P A P B A ?===+?+? 4．已知甲袋中有6只红球，4只白球；乙袋中有8只红球，6只白球。求下列事件的概率： (1) 随机取一只袋，再从该袋中随机取一球，该球是红球； (2) 合并两只袋，从中随机取一球，该球是红球。 解 (1) 记=B {该球是红球}，=1A {取自甲袋}，=2A {取自乙袋}，已知10/6)|(1=A B P ，14/8)|(2=A B P ，所以

二项分布中方差的计算

二项分布中方差的计算 假设ξ~B (n ,p ), 即k n k k n q p C k P -==}{ξ 考虑E [ξ(ξ-1)]=Eξ2-Eξ 而 ∑∑ ∑∑=----=-=-=--=-----?-?=--=-=-n k k n k k n n k k n k n k k n k n k k n k k n q p C p n n q p k n k n n n q p k n k n k k q p C k k E 2 222222 )1()]!2(2[)!2()!2()1()! (!! ) 1()1()]1([ξξ 令2-=k i 上式=222220 22 2 )1()1(np p n p n n q p C p n n n i i n i i n -=-=-∑-=--- 即2222np p n E E -=-ξξ, 再将E ξ=np 代入上式,得)1(222222p np p n np np p n E -+=+-=ξ 最后得npq np p np p n E E D =--+=-=22222)()1()(ξξξ 例1的分布图 例2的分布图 4.2 超几何分布 例1的图形：

例2的图形： 定义4.2 设N 个元素分为两类, 有N 1个属于第一类, N 2个属于第二类(N 1+N 2=N ). 从中不重复抽样取n 个, 令ξ表示这n 个中第一类元素的个数, 则ξ的分布称为超几何分布, ),....,1,0()(2 1n m C C C m P n N m n N m N == =-ξ 规定: 如n

2019年高考数学(理科)必考题突破讲座：第61讲 条件概率、n次独立重复试验与二项分布

第61讲 条件概率、n 次独立重复试验与二项分布 1．条件概率 (1)定义：设A ，B 为两个事件，且P (A )>0，称P (B |A )＝__P (AB ) P (A )__为在事件A 发生的条 件下，事件B 发生的条件概率． (2)性质：①0≤P (B |A )≤1；②如果B 和C 是两个互斥事件，则P (B ∪C |A )＝__P (B |A )＋P (C |A )__． 2．事件的相互独立性 (1)定义：设A ，B 为两个事件，如果P (AB )＝__P (A )·P (B )__，则称事件A 与事件B 相互独立． (2)性质：①若事件A 与B 相互独立，则P (B |A )＝__P (B )__，P (A |B )＝P (A )，P (AB )＝__P (A )·P (B )__． ②如果事件A 与B 相互独立，那么__A 与B __，__A 与B __，__A 与B __也都相互独立． 3．独立重复试验与二项分布 (1)独立重复试验 在__相同__条件下重复做的n 次试验称为n 次独立重复试验. A i (i ＝1,2，…，n )表示第i 次试验结果，则P (A 1A 2A 3…A n )＝__P (A 1)P (A 2)…P (A n )__． (2)二项分布 在n 次独立重复试验中，用 X 表示事件 A 发生的次数，设每次试验中事件A 发生的概率是p ，此时称随机变量X 服从二项分布，记作__X ～B (n ，p )__，并称p 为__成功概率__．在 n 次独立重复试验中，事件A 恰好发生k 次的概率为P (X ＝k )＝__C k n p k (1－p ) n － k __(k ＝0，1,2，…，n )．

贝叶斯预测方法

贝叶斯预测模型的概述 贝叶斯预测模型是运用贝叶斯统计进行的一种预测。贝叶斯统计不同于一般的统计方法，其不仅利用模型信息和数据信息，而且充分利用先验信息。 托马斯·贝叶斯（Thomas Bayes）的统计预测方法是一种以动态模型为研究对象的时间序列预测方法。在做统计推断时，一般模式是： 先验信息+总体分布信息+样本信息→后验分布信息 可以看出贝叶斯模型不仅利用了前期的数据信息，还加入了决策者的经验和判断等信息，并将客观因素和主观因素结合起来，对异常情况的发生具有较多的灵活性。这里以美国1960—2005年的出口额数据为例，探讨贝叶斯统计预测方法的应用。 Bayes预测模型及其计算步骤 此处使用常均值折扣模型，这种模型应用广泛而且简单，它体现了动态现行模型的许多基本概念和分析特性。 常均值折扣模型 对每一时刻t常均值折模型记为DLM{1，1，V，δ}，折扣因子δ，O<δ

推论2：μt的后验分布()～N [m t，C t]，其中f t = m t? 1,Q t = R t + V。 由于Rt=Ct-1+Wt=Ct-1/δ，故有W?t = C t? 1(δ? 1? 1) W 其计算步骤为： (1)R t = C?t / δ； (2)Q t = R t + V； (3)A t = R t / Q t； (4)f t? 1 = m t? 1； (5)e t?y t?f t? 1； (6)C t = A t V； (7)m t?m t? 1 + A t e t 计算实例 根据The SAS System for Windows 9．0所编程序，对美国出口额（单位：十亿元）变化进行了预测。选取常均值折扣模型和抛物线回归模型。 美国出口额的预测，预测模型的初始信息为m0=304，Co=72，V=0。Ol，δ=0。8得到的1960—2006年的预测结果。见表2中给出了预测的部分信息（1980—2006年的预测信息）。 通过The SAS System for Windows 9．0软件回归分析得到抛物线预测方程： 表示年份见表3给出了1980-2006年的预测信息。 计算结果分析 对预测结果的准确度采用平均绝对百分误差（MAPE）分析。公式如下： 根据表l和表2对1980-2005年出口额的预测结果可知，常均值折扣模型所得结果的平均绝对百分误差MAPE=8。1745％，而由抛物线回归模型所得结果的平均绝对百分误差为9。5077％。由此可见这组数据中，使用贝叶斯模型预测的结果更为精确。

二项分布、超几何分布数学期望与方差公式的推导

二项分布、超几何分布数学期望与方差公式的推导 高中教材中对二项分布和超几何分布数学期望与方差公式没有给出推导公式，现笔者给出一推导过程仅供参考。 预备公式一 11--=k n k n nC kC （1≥n ） ，利用组合数计算公式即可证明。 预备公式二 []2 2)()()(ξξξE E D -=，证明过程可见教材。 预备公式三 2 2)1()1(---=-k n k n C n n C k k （2,2≥≥k n ） ，利用组合数计算公式即可证明。 预备公式四 ),,,,(022110n k m k N k n m C C C C C C C C C k n m m k n k m n k m n k m n ≤≤∈=++++++--Λ，利用恒等 式m n n m x x x )1()1() 1(++=++的二项展开式中k x 的系数相等可证。 一、二项分布 在n 次独立重复试验中，每次试验中事件A 发生的概率为p （10<

全概率公式和贝叶斯公式练习题

例题讲解: 例题 1.市场上某产品由三家厂家提供，根据以往的记录，这三个厂家的次品率分别为，0.020.,0.01,0.03，三个厂家生产的产品所占的市场份额分别0.15,0.8,0.05.产品出厂后运到仓库，见面后再进入市场，设这三个厂家的产品在仓库是均匀混合 （1）在仓库中随机的取一个产品，求它的次品的概率。 （2）在仓库中随机的取一个产品，发现为次品，如果你是管理者，该如何追究三个厂家的责任？ 例题2 保险公司把被保险人分成三类”谨慎的”,”一般的”和”冒险的”，统计资料表明，上述三种人在一年内发生事故的概率依次为，0. 5. 0.15. 和0.30. 如果”谨慎的”被保险人占20%”一般的”，被保险人占50%，”冒失的”被保险人占30%，确认一个被保险人在一年内出事故的概率。

练习: 1.设某工厂有两个车间生产同型号家用电器，第一车间的次品率为0.15，第二车间的次品率为0.12，两个车间的成品都混合堆放在一个仓库，假设第1,2车间生产的成品比例为2:3，今有一客户从成品仓库中随机提一台产品，求该产品合格的概率。 解：设B={从仓库中随机提出的一台是合格品} A i ={提出的一台是第i 车间生产的}，i=1,2 则有分解B=A 1B ∪A 2B 由题意P(A1)=2/5,P(A2)=3/5,P(B|A1)=0.85,P(B|A2)=0.88 由全概率公式P(B)= P(A 1) P(B|A 1)+ P(A 2) P(B|A 2)=0.4*0.85+0.6*0.88=0.868. 2. 盒中有a 个红球，b 个黑球，今随机地从中取出一个，观察其颜色后放回，并加上同色球c 个，再从盒中第二次抽取一球，求第二次抽出的是黑球的概率。 解：设A={第一次抽出的是黑球}，B={第二次抽出的是黑球}，则B AB AB =+， 由全概率公式()()()()()P B P A P B A P A P B A =+， 由题意(),(|),(),(|)b b c a b P A P B A P A P B A a b a b c a b a b c +====++++++ 所以()()()()()()b b c ab b P B a b a b c a b a b c a b +=+=+++++++ 3. 设某公路上经过的货车与客车的数量之比为2:1，货车中途停车修理的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，求该汽车是货车的概率。 解：设B={中途停车修理}，A1={经过的是货车}，A2={经过的是客车}，则B=A 1B ∪A 2B ，由贝叶斯公式有 111112220.02()()3()0.80.21()()()()0.020.0133 P A P B A P A B P A P B A P A P B A ?===+?+? 4．已知甲袋中有6只红球，4只白球；乙袋中有8只红球，6只白球。求下列事件的概率： (1) 随机取一只袋，再从该袋中随机取一球，该球是红球； (2) 合并两只袋，从中随机取一球，该球是红球。 解 (1) 记=B {该球是红球}，=1A {取自甲袋}，=2A {取自乙袋}，已知10/6)|(1=A B P ，14/8)|(2=A B P ，所以 70411482110621)|()()|()()(2211=?+?= +=A B P A P A B P A P B P (2) 12 72414)(== B P

条件概率与超几何分布与二项分布练习题

条件概率及乘法公式练习题 1．一个袋中有9 张标有 1,2,3， , ， 9 的票，从中依次取两张，则在第一张是奇数的 条件下第二张也是奇数的概率（） 2．有一批种子的发芽率为 0.9，出芽后的幼苗成活率为 0.8，在这批种子中，随机抽取一 粒，求这粒种子能成长为幼苗的概率。 3．某种电路开关闭合后，会出现红灯或绿灯闪烁，已知开关第一次闭合后出现红灯的11 概率是 2 ，在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是 都出现红灯的概率。 3 ，求两次闭合4．市场供应的灯泡中，甲厂产品占有70%，乙厂产品占有30%，甲厂产品的合格率为95%，乙厂产品的合格率为80%。现从市场中任取一灯泡，假设A=“甲厂生产的产品”，A=“乙厂生产的产品” ， B=“合格灯泡”，B =“不合格灯泡”，求： （1） P(B|A) ；（ 2）P( B |A) ；（ 3）P(B| A ) ；（ 4） P(B | A ). 超几何分布及二项分布练习题 1.一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5 的 5 个红球与编号为1,2,3,4 的 4个白球，从中任意取出3个球. （Ⅰ）求取出的3个球颜色相同且编号是三个连续整数的概率； （Ⅱ）求取出的3个球中恰有 2 个球编号相同的概率； 2.今年雷锋日，某中学从高中三个年级选派 4 名教师和 20 名学生去当雷锋志愿者，学生的名额分 配如下： 高一年级10 人高二年级 6 人 高三年级 4 人 （ I ）若从 20 名学生中选出 3 人参加文明交通宣传，求他们中恰好有 1 人是高一年级学生的概率； （ II ）若将 4 名教师安排到三个年级（假设每名教师加入各年级是等可能的，且各位教师的选择是相互独立的），记安排到高一年级的教师人数为X ，求随机变量X 的分布列和数学期望 .

贝叶斯统计方法

贝叶斯方法 贝叶斯分类器是一种比较有潜力的数据挖掘工具，它本质上是一种分类手段，但是它的优势不仅仅在于高分类准确率，更重要的是，它会通过训练集学习一个因果关系图（有向无环图）。如在医学领域，贝叶斯分类器可以辅助医生判断病情，并给出各症状影响关系，这样医生就可以有重点的分析病情给出更全面的诊断。进一步来说，在面对未知问题的情况下，可以从该因果关系图入手分析，而贝叶斯分类器此时充当的是一种辅助分析问题领域的工具。如果我们能够提出一种准确率很高的分类模型，那么无论是辅助诊疗还是辅助分析的作用都会非常大甚至起主导作用，可见贝叶斯分类器的研究是非常有意义的。 与五花八门的贝叶斯分类器构造方法相比，其工作原理就相对简单很多。我们甚至可以把它归结为一个如下所示的公式： 选取其中后验概率最大的c，即分类结果，可用如下公式表示

贝叶斯统计的应用范围很广，如计算机科学中的“统计模式识别”、勘探专家所采用的概率推理、计量经济中的贝叶斯推断、经济理论中的贝叶斯模型等。 上述公式本质上是由两部分构成的：贝叶斯分类模型和贝叶斯公式。下面介绍贝叶斯分类器工作流程： 1．学习训练集，存储计算条件概率所需的属性组合个数。 2．使用1中存储的数据，计算构造模型所需的互信息和条件互信息。 3．使用2种计算的互信息和条件互信息，按照定义的构造规则，逐步构建出贝叶斯分类模型。 4．传入测试实例 5．根据贝叶斯分类模型的结构和贝叶斯公式计算后验概率分布。6．选取其中后验概率最大的类c，即预测结果。 一、第一部分中给出了7个定义。 定义1 给定事件组，若其中一个事件发生，而其他事件不发生，则称这些事件互不相容。 定义 2 若两个事件不能同时发生，且每次试验必有一个发生，则称这些事件相互对立。 定义 3 若定某事件未发生，而其对立事件发生，则称该事件失败 定义4 若某事件发生或失败，则称该事件确定。 定义 5 任何事件的概率等于其发生的期望价值与其发生所得到

二项分布方差公式推导

二项分布方差公式推导 若ξ～B(n,p)，q=1-p ，求证D ξ=npq ∵E ξ=np ， kC n k p k q n-k =n p 11 k n C --p k-1q n-k , kk C n k p k q n-k =np[(k-1)11 k n C --p k-1q n-k ＋11k n C --p k-1q n-k ] =np[(n －1)p 22k n C --p k-2q n-k ＋11k n C --p k-1q n-k ] 而D ξ=22()E E ξξ-， ∴D ξ=(1×1×C n 1p 1q n-1＋2×2 C n 2p 2q n-2＋…＋k ×k C n k p k q n-k ＋…＋n ×n C n n p n q 0)2() np - =np(1×C n-10p 0q n-1＋2C n-11p 1q n-2＋3C n-12p 2q n-2＋…＋ k C n-1k-1p k-1q n-k ＋…＋n C n-1n-1p n-1q 0)－2np E ξ＋n 2p 2(p ＋q)n =np{[0×C n-10p 0q n-1＋1C n-11p 1q n-2＋2C n-12p 2q n-2＋…＋ (k-1) C n-1k-1p k-1q n-k ＋…＋(n-1)C n-1n-1p n-1q 0]＋(C n-10p 0q n-1＋ C n-11p 1q n-2＋C n-12p 2q n-2＋…＋C n-1k-1p k-1q n-k ＋…＋ C n-1n-1p n-1q 0)}2()np - =np[E η＋(p ＋q)n-1] 2() np - =np[(n －1)p ＋1] 2() np - =np(1－p) =npq .

条件概率与超几何分布及二项分布练习题()

条件概率及乘法公式练习题 1.一个袋中有9张标有1,2,3，…，9的票，从中依次取两张，则在第一张是奇数的 条件下第二张也是奇数的概率( ) 2.有一批种子的发芽率为0.9，出芽后的幼苗成活率为0.8，在这批种子中，随机抽 取一粒，求这粒种子能成长为幼苗的概率。 3?某种电路开关闭合后，会出现红灯或绿灯闪烁，已知开关第一次闭合后出现红灯的 1 1 概率是2，在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是3，求两次闭合都出现红灯的概率。 4.市场供应的灯泡中，甲厂产品占有70%乙厂产品占有30%甲厂产品的合格率为95% 乙厂产品的合格率为80%现从市场中任取一灯泡，假设A= “甲厂生产的产品” ，A = “乙厂生产的产品”，B=“合格灯泡”，B = “不合格灯泡”，求： (1) P(B|A) ; (2) P( B |A) ; (3) P(B| A ) ; ( 4) P( B | A). 超几何分布及二项分布练习题 1. 一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5 的5个红球与编号为1,2,3,4 的4个白球，从中任意取出3个球. (I)求取出的3个球颜色相同且编号是三个连续整数的概率； (n)求取出的3个球中恰有2个球编号相同的概率； 2.今年雷锋日，某中学从高中三个年级选派4名教师和20名学生去当雷锋志愿者，学生的 名额分配如下： (I )若从20名学生中选出3人参加文明交通宣传，求他们中恰好有1人是高一年级学生的概率； (II )若将4名教师安排到三个年级 (假设每名教师加入各年级是等可能的，且各位教师

的选择是相互独立的)，记安排到高一年级的教师人数为X，求随机变量X的分布列和数学期望.