泊松分布表

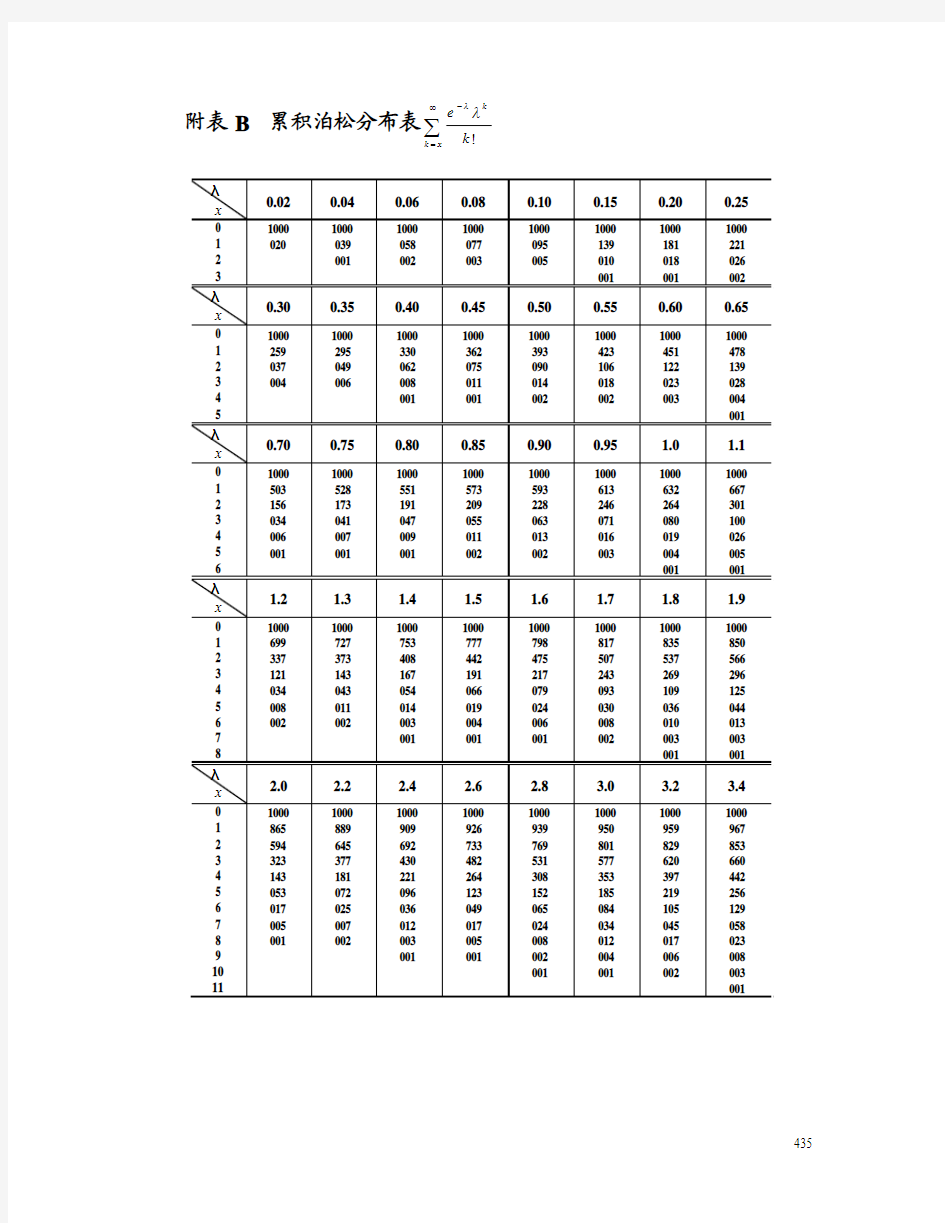
附表B累积泊松分布表∑∞

=

-x

k

k k

e

!

λλ

435

附表B累积泊松分布表(续)

附表B累积泊松分布表(续)

436

437

附表B累积泊松分布表(续)

438

卡方分布概念及表和查表方法

若n个相互独立的随机变量ξ?，ξ?，...,ξn，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。 目录 1简介 2定义 3性质 4概率表 简介 分布在数理统计中具有重要意义。分布是由阿贝(Abbe)于1863年首先提出的，后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来，是统计学中的一个非常有用的著名分布。 定义 若n个相互独立的随机变量ξ?、ξ?、……、ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为分布（chi-square distribution）， 卡方分布是由正态分布构造而成的一个新的分布，当自由度很大时，分布近似为正态分布。

对于任意正整数x，自由度为的卡方分布是一个随机变量X的机率分布。 性质 1) 分布在第一象限内，卡方值都是正值，呈正偏态（右偏态），随着参数 的增大，分布趋近于正态分布；卡方分布密度曲线下的面积都是1。 2) 分布的均值与方差可以看出，随着自由度的增大，分布向正无穷方向延伸（因为均值越来越大），分布曲线也越来越低阔（因为方差越来越大）。 3）不同的自由度决定不同的卡方分布，自由度越小，分布越偏斜。 4) 若互相独立，则：服从分布，自由度为 。 5) 分布的均数为自由度，记为 E( ) = 。 6) 分布的方差为2倍的自由度( )，记为 D( ) = 。 概率表 分布不象正态分布那样将所有正态分布的查表都转化为标准正态分布去查，在 分布中得对每个分布编制相应的概率值，这通过分布表中列出不同的自由度来表示， 查分布概率表时，按自由度及相应的概率去找到对应的值。如上图所示的单侧概率(7)=的查表方法就是，在第一列找到自由度7这一行，在第一行中找到概率这一列，行列的交叉处即是。 表中所给值直接只能查单侧概率值，可以变化一下来查双侧概率值。例如，要在自由度为7的卡方分布中，得到双侧概率为所对应的上下端点可以这样来考虑：双侧概率指的是在

概率论与数理统计课程报告：泊松分布及其在实际中的应用

泊松分布及其在实际中的应用 摘要：本文从泊松分布的定义和基本性质出发，举例讨论了泊松分布在实际中的重要应用。 关键字：泊松分布；应用；运筹学；分子生物学；核衰变 泊松分布是法国数学家泊松于1837年引入的，是概率论中的几大重要分布之一。作为一种常见的离散型随机变量的分布，其在实际中有着非常广泛的应用。 1泊松分布的定义及基本知识 1.1定义： （1）若随机变量X 的分布列为 ）， ?=>= =-,2,1,0(0,! )(k k e k X P k λλλ 则称X 服从参数为λ的泊松分布，并用记号X~P(λ)表示。 （2）泊松流： 随机质点流：随机现象中源源不断出现的随机质点构成的序列。 若质点流具有平稳性、无后效性、普通性, 则称该质点流为泊松事件流(泊松流)。 例如某电话交换台收到的电话呼叫数; 到某机场降落的飞机数; 一个售货员接待的顾客数等这些事件都可以看作泊松流。 1.2有关泊松分布的一些性质 （1）满足分布列的两个性质：P(X=k)≥0(k=0,1,2,…）， 且有 1! ! )(0 =?====-∞ =-∞=∞ =-∑∑∑ λλλ λ λλe e k e k e k X P k k k o k k . （2）若随机变量X 服从参数为λ的泊松分布，则X 的期望和方差分别为：E （X)=λ; D(X)=λ. （3）以n ，p 为参数的二项分布，当n →∞，p →0时，使得np=λ保持为正常数，则 λλ--→ -e k p p C k k n k k n ! ) 1(对于k=0,1,2，…一致成立。 由如上定理的条件λ=np 知，当n 很大时，p 很小时，有下面的近似公式 λλ--→ -=e k p p C k P k k n k k n n ! ) 1()( 2泊松分布的应用 对于试验成功概率很小而试验次数很多的随机过程, 都可以很自然的应用于泊松分布的理论。在泊松分布中的概率表达式只含一个参数λ，减少了对参数的确定与修改工作量, 模型构建比较简单, 具有很重要的实际意义。 以下具体举例说明泊松分布在实际中的重要应用。 （1）泊松分布在经济生活中的应用： 泊松分布是经济生活中的一种非常重要的分布形式，尤其是经常被运用在运筹学研究中的一个分布模型。如物料订单的规划，道路交通信号灯的设计，生产计划的安排，海港发

二项分布概念及图表和查表方法

目录 1定义 ?统计学定义 ?医学定义 2概念 3性质 4图形特点 5应用条件 6应用实例 定义 统计学定义 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当 时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。

考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。如果进行次伯努利试验，取得成功次数为 的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 式中的n为独立的伯努利试验次数，π为成功的概率，（1-π）为失败的概率，X为在n次伯努里试验中出现成功的次数，表示在n次试验中出现X的各种组合情况，在此称为二项系数（binomial coefficient）。 所以的含义为：含量为n的样本中，恰好有X例阳性数的概率。 概念 二项分布（Binomial Distribution），即重复n次的伯努利试验（Bernoulli Experiment），用ξ表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望：Eξ=np； 方差：Dξ=npq； 其中q=1-p 证明：由二项式分布的定义知，随机变量X是n重伯努利实验中事件A发生的次数，且在每次试验中A发生的概率为p。因此，可以将二项式分布分解成n个相互独立且以p为参数的（0-1）分布随机变量之和。 设随机变量X（k）(k=1,2,3...n)服从（0-1）分布，则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立，所以期望：

泊松分布的概念及表和查表方法

目录 1命名原因 2分布特点 3关系 4应用场景 5应用示例 6推导 7形式与性质 命名原因 泊松分布实例

泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（discrete probability distribution）。泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）命名的，他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。 分布特点 泊松分布的概率函数为： 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。 泊松分布的期望和方差均为特征函数为 关系 泊松分布与二项分布 泊松分布 当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦时，就可以用泊松公式近似得计算。 事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。 应用场景 在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。 应用示例

二项分布概念及图表和查表方法

二项分布概念及图表 二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。 目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例 定义 统计学定义 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当 时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。 考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。如果进行次伯努利试验，取得成功次数为的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 二项分布公式 P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。

06二项分布及泊松分布

●Bernoulli 试验（Bernoulli T est）： 将感兴趣的事件A出现的试验结果称为“成功”，事件A不出现的试验结果称为“失败”，这类试验就称为Bernoulli 试验 ●二项分布（binomial distribution）： 是指在只会产生两种可能结果如阳性或阴性之一的n次独立重复试验中，当每次试验的阳性概率π保持不变时，出现阳性次数X=0,1,2，…，n的一种概率分布。 ●Poisson分布（Poisson distribution）： 随机变量X服从Poisson分布式在足够多的n次独立试验中，X取值为1,2,…,的相应概率为 …的分布。 ★二项分布成立的条件： ①每次试验只能是互斥的两个结果之一；②每次试验的条件不变；③各次试验独立。 ★二项分布的图形： 当∏=0.5，二项分布图形是对称的，当∏不等于0.5，图形是偏态的，随着n增大，图形趋于对称。当n趋于无穷大时，只有∏不太靠近0或者1，二项分布近似正态分布。 ★二项分布的应用 总体率的区间估计，样本率与总体率比较，两样本率的比较 ★Poisson 分布的应用 总体均数的区间估计，样本均数与总体均数的比较，两个样本均数的比较：两个样本计数均较大时，可根据Poisson 分布的正态近似性对其进行u 检验。 ★Poisson 分布成立的条件： ①平稳性：X 的取值与观察单位的位置无关，只与观察单位的大小有关；②独立增量性：在某个观察单位上X 的取值与前面各观察单位上X 的取值无关；③普通性：在充分小的观察单位上X 的取值最多为1。 Poisson 分布，X～P（μ），X 的均数μX =μ，X的方差σ2 =μ，X的标准差σX ★Poisson分布的性质 1、总体均数λ与总体方差相等是泊松分布的重要特点。 2、当n增大，而∏很小，且n∏=λ总体均数时，二项分布近似泊松分布。 3、当总体均数增大时，泊松分布渐近正态分布，一般而言，总体均数》20时，泊松分布资料做为正态分布处理。 4、泊松分布具有可加性。 ★泊松分布的图形 当总体均数越小，分布就越偏态，当总体均数越大，泊松分布就越趋近正态分布。当总体均数小于等于1时，随X取值的变大，P(X)值反而变小；当总体均数大于1时，P(X)值先增大而后变小，若总体均数取整数时，则P(X)在X=总体均数，和X=总体均数—1取得最大值。 ★二项分布和泊松分布的特性 1．可加性 二项分布和Poisson 分布都具有可加性。 如果X1，X2，?Xk 相互独立，且它们分别服从以ni，p（i=1,2, ?,k）为参数的二项分 布，则X=X1＋X2＋?＋Xk 服从以n，p（n=n1+n2+?+nk）为参数的二项分布。如果X1，X2，?，Xk相互独立，且它们分别服从以μi（i=1,2, ?,k）为参数的Poisson 分布，则X=X1＋X2＋?＋Xk服从以μ（μ=μ1+μ2+?+μk）为参数的Poisson 分布。 2．近似分布

泊松过程与泊松分布的基本知识

泊松过程与泊松分布的基本知识泊松过程是随机过程的一个经典模型，是一种累积随机事件的发生次数的独立增量过程。也就是说，每次事件的发生是相互独立的。那么泊松分布和泊松过程又什么关系呢？可以说泊松分布是描述稀有事件的统计规律，即可以描述一段时间内发生某个次数的概率。而泊松过程呢，就适合刻画“稀有事件流”的概率特性。 比较：泊松分布 泊松过程的主要公式： 其实没多少不一样对不对？不一样的是泊松过程是一个可以查看在时间t内发生次数的概率，这个t是可变的。泊松分布则是给定了时间。 泊松过程的关键在于，它的到达间隔序列Tn，即每两次发生的时间是服从的独立同指数分布的。如果每次发生的间隔时间不服从指数分布，那么这个随机过程就会更一般化，我们成为是更新过程，这也是随机过程的推广。 泊松过程分为齐次泊松过程和非齐次泊松过程，齐次的意思很简单，就是说过程并不依赖于初始时刻，强度函数是一个常数，从上面的公式也看得出来。而非齐次则是变成了,这意味着什么呢？这以为着随着与时间的改变，强度是会改变的，改变服从强度函数，说了这

么久，强度究竟是个什么概念？强度的意思就是泊松过程的该事件发生的频率，或者说快慢，泊松分布中我们知道期望就是,实际含义就是，在一段时间内，发生的次数平均水平是次。 复合泊松过程：泊松过程我们已经知道，用描述一段时间累积发生的次数，但是如果每次发生带来的后果都是不一样的，我们怎么描述这个过程呢？比如，火车站到达的乘客是服从泊松过程的，但是每个乘客携带有不同重量的行李，我们如何刻画在[0,t]时间内行李总重量呢，这个过程就是复合泊松过程。复合泊松过程的均值函数和方差函数一般可以用全期望和全方差公式进行计算，因为简单泊松过程的期望很容易求。 更新过程： 上文已经说到，更新过程作为泊松过程的推广，更具有一般性，那么在讨论更新过程时，我们更多地讨来更新函数，更新函数是更新过程的均值函数m(t)=E[N(t)]，怎么理解呢，就是说需要用t时刻的累积计数的期望特性来表达更新过程。有一条定理： 这个定理是可以证明的，Fn（t）是分布函数，就是说：在t时刻，更新函数值就是在这个时刻，n取遍所有值的分布之和。 那么是否可以这样理解，更新过程和泊松过程的区别就是更新间隔序列不同，那么如果已知了更新间隔序列的概率密度函数，就可以求解该过程的更新函数了，详细的推导就不写了。扔结论出来：对间隔序列概率密度函数做拉氏变换得到Lf(s),然后求 Lm(s)=Lf(s)/s(1-Lf(s)),再对Lm(s)进行逆变换，就得到了m(t),这就是更新函数。

二项分布概念及图表和查表方法

目录 1 定义 ?统计学定义 ?医学定义 2 概念 3 性质 4 图形特点 5 应用条件 6 应用实例 定义 统计学定义 在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当 时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。 医学定义 在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。

考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。如果进行次伯努利试验，取得成功次数为的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X) 二项分布公式 表示随机试验的结果。 二项分布公式 如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p) 期望：Eξ=np； 方差：Dξ=npq； 其中q=1-p 证明：由二项式分布的定义知，随机变量X是n重伯努利实验中事件A发生的次数，且在每次试验中A发生的概率为p。因此，可以将二项式分布分解成n个相互独立且以p为参数的（0-1）分布随机变量之和。 设随机变量X（k）(k=1,2,3...n)服从（0-1）分布，则X=X(1)+X(2)+X(3)....X(n). 因X(k)相互独立，所以期望：

泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法 Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。 中文名泊松分布外文名poisson distribution 分类数学时间1838年 台译卜瓦松分布提出西莫恩·德尼·泊松 目录 1命名原因 2分布特点 3关系 4应用场景 5应用示例 6推导 7形式与性质

命名原因 泊松分布实例 泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（discrete probability distribution）。泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）命名的，他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。 分布特点 泊松分布的概率函数为： 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。 泊松分布的期望和方差均为特征函数为 关系 泊松分布与二项分布 泊松分布

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦时，就可以用泊松公式近似得计算。 事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。 应用场景 在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。 应用示例 泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷数，显微镜下单位分区内的细菌分布数等等。 观察事物平均发生m次的条件下，实际发生x次的概率P（x）可用下式表示： 例如采用㎡紫外线照射大肠杆菌时，每个基因组（～4×106核苷酸对）平均产生3个嘧啶二体。实际上每个基因组二体的分布是服从泊松分布的，将取如下形式： …… 是未产生二体的菌的存在概率，实际上其值的5%与采用㎡照射时的大肠杆菌uvrA-株，recA-株（除去既不能修复又不能重组修复的二重突变）的生存率是一致的。由于该菌株每个基因组有一个二体就是致死量，因此就意味着全部死亡的概率。 推导

泊松分布及其应用研究

泊松分布及其应用研究 Prepared on 22 November 2020

湖南科技大学 信息与电气工程学院 《课程论文》 题目：泊松分布及其应用研究 专业：通信工程 班级： 13级3班 姓名：黄夏妮 学号： 目录 一、摘要 (1) 二、泊松分布的概念 (2) 三、计数过程为广义的泊松过程 (4) 四、泊松分布及泊松分布增量 (5) 五、泊松分布的特征 (5) 六、泊松分布的应用 (6) 七、基于MATLAB的泊松过程仿真 (8) 八、参考文献 (12)

摘要 作为一种常见的离散型随机变量的分布,泊松分布日益显示其重要性,成为概率论中最重要的几个分布之一。服从泊松分布的随机变量是常见的,它常与时间单位的计数过程相联系。 在现实生活中应用更为广泛,如数学建模、管理科学、运筹学及自然科学、概率论等等。并且在某些函数关系起着一种重要作用。例如线性的、指数的、三角函数的等等。同样, 在为观察现象构造确定性模型时, 某些概率分布也经常出现。泊松分布作为大量试验中稀有事件出现的频数的概率分布的数学模型, 它具有很多性质。为此本文讲述了泊松分布的一些性质, 并讨论了这些性质在实际生活中的重要作用。

二、泊松分布的概念： 定义1 设随机变量X 的可能取值为,,2,1,0 且 {}0,,2,1,0,! >===-λλ k e k x k X P k 为常数。 则称X 服从参数为λ的泊松分布,记作X ～ D(λ) 。 定义2 设ε是任意一个随机变量,称 )t (- e t)(it +∞<<∞=Φε是ε的特征函数。 主要结论： 定理1 如果X 是一个具有以λ为参数的泊松分布,则E( X) = λ且D ( X) =λ。 证明 设X 是一随机变量,若 ] X) E( - X [ E{2}存在,则称它为X 的方差,记作D( X) ,即 ] X) E( - X [ E{ X) D(2}=。设X 服从泊松分布D ( X) ,即有: 则()()λλλλλλλλ λ=?=-==- ∞ =--∞ =-∑∑ e e k e k e k X E k k k k 11 0!1! 从而()() () λλλλλλλ λ +=-+-==-∞ =-∞ =--∞ =∑ ∑ ∑2122 2 2 !1!2! e k e k e k k X E k k k k k k 故λλλλ - X) E( - ) X E( X) D(2222=+== 定理2 设随机变量) , ,2 1 n ( x n =服从二项分布,其分布律为 {}n k p p C k x P k n n k n k n n ,,2,1,0,)1( =-==-。 又设0>=λn np 是常数,则{}λλ-∞ →==e k k x P k n n ! lim 。 证明 由λ=n np 得: 显然,当k = 0 时,故λ-n e k} x P{→=。当k ≥1 且k → ∞时,有

二项分布表

附录2 附表 附表1 二项分布表 0{}(1)x k n k n P X x p p k k ?=?? ≤=????? ∑ p n x 0.001 0.002 0.0030.005 0.01 0.02 0.03 0.05 0.10 0.15 0.20 0.25 0.30 2 0 0.9980 0.9960 0.99400.9900 0.9801 0.96040.94090.90250.81000.72250.6400 0.5625 0.4900 2 1 1.0000 1.0000 1.00001.0000 0.9999 0.99960.99910.99750.99000.97750.9600 0.9375 0.9100 3 0 0.9970 0.9940 0.99100.9851 0.9703 0.94120.91270.85740.72900.61410.5120 0.4219 0.3430 3 1 1.0000 1.0000 1.00000.9999 0.9997 0.99880.99740.99280.97200.93930.8960 0.8438 0.7840 3 2 1.0000 1.0000 1.00001.00000.99990.99900.99660.9920 0.9844 0.9730 4 0 0.9960 0.9920 0.98810.9801 0.9606 0.92240.88530.81450.65610.52200.4096 0.3164 0.2401 4 1 1.0000 1.0000 0.99990.9999 0.9994 0.99770.99480.98600.94770.89050.8192 0.7383 0.6517 4 2 1.00001.0000 1.0000 1.00000.99990.99950.99630.98800.9728 0.9492 0.9163 4 3 1.00001.00000.99990.99950.9984 0.9961 0.9919 5 0 0.9950 0.9900 0.98510.9752 0.9510 0.90390.85870.77380.59050.44370.3277 0.2373 0.1681 5 1 1.0000 1.0000 0.99990.9998 0.9990 0.99620.99150.97740.91850.83520.7373 0.6328 0.5282 5 2 1.00001.0000 1.0000 0.99990.99970.99880.99140.97340.9421 0.8965 0.8369 5 3 1.00001.00001.00000.99950.99780.9933 0.9844 0.9692 5 4 1.00000.99990.9997 0.9990 0.9976 6 0 0.9940 0.9881 0.98210.9704 0.9415 0.88580.83300.73510.53140.37710.2621 0.1780 0.1176 6 1 1.0000 0.9999 0.99990.9996 0.9985 0.99430.98750.96720.88570.77650.6554 0.5339 0.4202 6 2 1.0000 1.00001.0000 1.0000 0.99980.99950.99780.98420.95270.9011 0.8306 0.7443 6 3 1.00001.00000.99990.99870.99410.9830 0.9624 0.9295 6 4 1.00000.99990.99960.9984 0.9954 0.9891 6 5 1.00001.00000.9999 0.9998 0.9993 7 0 0.9930 0.9861 0.97920.9655 0.9321 0.86810.80800.69830.47830.32060.2097 0.1335 0.0824 7 1 1.0000 0.9999 0.99980.9995 0.9980 0.99210.98290.95560.85030.71660.5767 0.4449 0.3294 7 2 1.0000 1.00001.0000 1.0000 0.99970.99910.99620.97430.92620.8520 0.7564 0.6471 7 3 1.00001.00000.99980.99730.98790.9667 0.9294 0.8740 7 4 1.00000.99980.99880.9953 0.9871 0.9712 7 5 1.00000.99990.9996 0.9987 0.9962 7 6 1.00001.0000 0.9999 0.9998 8 0 0.9920 0.9841 0.97630.9607 0.9227 0.85080.78370.66340.43050.27250.1678 0.1001 0.0576 8 1 1.0000 0.9999 0.99980.9993 0.9973 0.98970.97770.94280.81310.65720.5033 0.3671 0.2553 8 2 1.0000 1.00001.0000 0.9999 0.99960.99870.99420.96190.89480.7969 0.6785 0.5518 8 3 1.0000 1.00000.99990.99960.99500.97860.9437 0.8862 0.8059 - 262 -

泊松分布的应用

泊松分布的应用

泊松分布的应用 摘要 泊松分布是指一个系统在运行中超负载造成的失效次数的分布形式。它是高等数学里的一个概念,属于概率论的范畴,是法国数学家泊松在推广伯努利形式下的大数定律时,研究得出的一种概率分布,因而命名为泊松分布。 作为一种常见的离散型随机变量的分布,泊松分布日益显示其重要性,成为概率论中最重要的几个分布之一。服从泊松分布的随机变量是常见的,它常与时间单位的计数过程相联系。 在现实生活中应用更为广泛,如数学建模、管理科学、运筹学及自然科学、概率论等等。并且在某些函数关系起着一种重要作用。例如线性的、指数的、三角函数的等等。本文对泊松分布产生的过程、定义和性质做了简单的介绍，研究了泊松分布的一些性质, 并讨论了这些性质在实际生活中的重要作用。 关键词：泊松过程；泊松分布；定义；定理；应用；

一、 计数过程为广义的泊松过程 1．计数过程 设)} 0, [ T t , t)( {N X T ∞=∈=为一随机过程, 如果 t )( N 是取非负整数值的随机变量,且满足s < t 时, t)( s) ( N ≤,则称)} 0, [ T t , t)( {N X T ∞=∈=为计数过程。 将增量 t t 0 , t), t ( N ) t ( N - t)( N 000<≤?=,它表示时间间隔 t), t [ 0内出现的质点数。“在 t), t [ 0内出现k 个质点”,即k} t), t ( {N 0=是一随机事件,其概率记为 2 0,1, k , k} t), t ( P{N t), t ( P 00K ===总之,对某种随机事件的来到数都可以得到一个计数过程,而同一时刻只能至多发生一个来到的就是简单计数过程。 2．泊松过程 计数过程0} t , t)( {N ∈称为强度为λ的泊松过程,如果满足条件: (1)在不相重叠的区间上的增量具有独立性; (2)0 (0) N =; (3)对于充分小的, t)( O t 1} t) t t,( P{N t) t t,( P 1?+?==?+=?+λ其中常数 0>λ,称为过程)(t N 的强度。 (4)对于充分小的Δt (){}()t j t t t N P t t t P j j j ?==?+=?+∑∑∞ =∞=ο2 2 ,),( 亦即对于充分小的t ?,在()t t t ?+,或2个以上质点的概率与出现一个质点的概率相对可以忽略不计。了解泊松过程,就很容易去了解泊松分布的相关性质,其实泊松分布就是在泊松过程当中每单位的时间间隔内出现质点数目的计数。 二、 泊松分布的概念： 泊松分布常用于描述单位时间、单位平面或单位空间中罕见“质点”总数的随机分布规律。 定义1 设随机变量X 的可能取值为,,2,1,0 且 {}0,,2,1,0,! >===-λλ k e k x k X P k 为常数。

概率统计论 浅谈泊松分布

浅谈泊松分布 班级：XXX 姓名：XXX 学号：XXX

浅谈泊松分布当一个随机事件，以固定的平均瞬时速率λ

二项概率的泊松逼近 如果∞→n ，0→p 使得λ=np 保持为正常数，则 λλ--→-e k p p C k k n k k n !)1( 对k = 0,1,2,…一致地成立。

2.1泊松分布使用范围 泊松分布主要用于描述在单位时间(空间)中稀有事件的发生数. 即需满足以下四个条件： 1. 给定区域内的特定事件产生的次数，可以是根据时间，长度，面积来定义； 2. 各段相等区域内的特定事件产生的概率是一样的； 3. 各区域内，事件发生的概率是相互独立的；

4. 当给定区域变得非常小时，两次以上事件发生的概率趋向于0。 2.2泊松分布的性质 1. 泊松分布的均数与方差相等，即m =2σ 2．泊松分布的可加性 如果1x ，2x ，3x …k x 相互独立，且它们分别服从以1λ，2λ，3λ…k λ为参数的泊松分布，则k X X X X T ++++= 321也服从泊松分布，其参数为k λλλλ++++ 321。 3.泊松分布的应用 )0(P 是未产生二体的菌的存在概率，实际上其值的5%与采用2/05.0m J 照射时的大肠杆菌uvrA -株，recA -株（除去既不能修复又不能重组修复的二重突变）的生存率是一致的。由于该菌株每个基因

组有一个二体就是致死量，因此)1(P ，)2(P ……就意味着全部死亡的概率。 3.2泊松分布在医学统计上的应用 在遗传学上，计算遗传图距的基本方法是建立在重组率基础上的，根据重组率的大小作出有关基因间的距离，绘制线性基因图；可是当研究的两个基因间的距离相对较远，在它们之间可能发生双交换、三交换、四交换甚至更高数目的交换，而形成的配子总有一半是非重组型的。若简单的把重组率看作交换率，显然交换率降低了，图距也随之缩小。这里可以用泊松分布原理来描述减数分裂过程中染色体上某区段交换的分布。在图距计算中，x 表示交换数，m 表示对总样本来说每进行一次减数分裂两基因 间的平均交换数，而基因间不发生交换的概率为m m e e m P --==! 0)0(0 ，基因间至少发生一次交换的概率为m e P P --=-=1)0(1。由此可计算两基因间的交换率和重组率。进而可更科学的作出遗传图。 3.3 泊松分布在交通运输上的应用 道路是行驶各种车辆的通道。为了给编制交通建设规划提供可靠的依据和保证道路上的车能安全而有效地通行, 道路工作者必须对道路上的车流进行实地调查和统计分析以便掌握车流的变化规律。数理统计方法是对交通流分布进行研究的有效而实际可行的方法。通常把在单位时间内通过道路上某一地点的车辆叫做交通流。对于时间间隔极短,并非是高密度的交通流的分布状态, 它常常是服从“概率论” 中的“ 泊松分布” 规律的。 如用简单例子表示，取通过某一地点车辆的时间作为时间数轴, 在数轴上划出给定时间间隔和该时间间隔内通过的车辆数目,譬如, 以20秒的时间间隔的数轴为例, 在20~0秒内,一辆车也没有通过, 在40~20秒间隔内,有二辆车通过, 在60~40秒间隔内, 有一辆车通过, 等等。这样在实地进行大量观测就可以的到某一时间间隔内的随机来车数目和该时间间隔内出现该车辆数的次数, 从而按泊松分布公式求算在给定时间间隔内在某一地点通过γ辆车的概率)(γP 。 参考文献 1． 戴维 M. 莱文等.《以EXCEL 为决策工具的商务统计》.机械工业出版社，2009 2．庄军、林奇英《泊松分布在生物学中的应用》.激光生物学报.2007年第16卷第5期. 3．薛珊荣 《“泊松分布”在交通工程中的应用》.湖南大学学报.1995年第8卷第2期.

数学分布(泊松分布、二项分布、正态分布、均匀分布、指数分布)生存分析贝叶斯概率公式全概率公式(新)

数学期望：随机变量最基本的数学特征之一。它反映随机变量平均取值的大小。又称期望或均值。它是简单算术平均的一种推广。例如某城市有10万个家庭，没有孩子的家庭有1000个，有一个孩子的家庭有9万个，有两个孩子的家庭有6000个，有3个孩子的家庭有3000个，则此城市中任一个家庭中孩子的数目是一个随机变量，记为X，它可取值0，1，2，3，其中取0的概率为0.01，取1的概率为0.9，取2的概率为0.06，取3的概率为0.03，它的数学期望为0×0.01＋1×0.9＋2×0.06＋3×0.03等于1.11，即此城市一个家庭平均有小孩1.11个，用数学式子表示为：E(X)=1.11。 也就是说，我们用数学的方法分析了这个概率性的问题，对于每一个家庭，最有可能它家的孩子为1.11个。 可以简单的理解为求一个概率性事件的平均状况。 各种数学分布的方差是： 1、一个完全符合分布的样本 2、这个样本的方差 概率密度的概念是：某种事物发生的概率占总概率(1)的比例,越大就说明密度越大。比如某地某次考试的成绩近似服从均值为80的正态分布，即平均分是80分，由正态分布的图形知x=80时的函数值最大，即随机变量在80附近取值最密集，也即考试成绩在80分左右的人最多。 下图为概率密度函数图(F(x)应为f(x)，表示概率密度)：

离散型分布：二项分布、泊松分布 连续型分布：指数分布、正态分布、X2分布、t分布、F分布 抽样分布 抽样分布只与自由度，即样本含量（抽样样本含量）有关 二项分布（binomial distribution）：例子抛硬币 1、重复试验（n个相同试验，每次试验两种结果，每种结果概率恒定———— 伯努利试验） 2、

泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法 目录 1命名原因 2分布特点 3关系 4应用场景 5应用示例 6推导 7形式与性质

命名原因 泊松分布实例 泊松分布（Poisson distribution），台译卜瓦松分布（法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等），是一种统计与概率学里常见到的离散机率分布（discrete probability distribution）。泊松分布是以18～19 世纪的法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）命名的，他在1838年时发表。这个分布在更早些时候由贝努里家族的一个人描述过。 分布特点 泊松分布的概率函数为： 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。 泊松分布的期望和方差均为特征函数为 关系 泊松分布与二项分布 泊松分布 当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

事实上，泊松分布正是由二项分布推导而来的，具体推导过程参见本词条相关部分。 应用场景 在实际事例中，当一个随机事件，例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位（在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性）。 应用示例 泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷数，显微镜下单位分区内的细菌分布数等等。 观察事物平均发生m次的条件下，实际发生x次的概率P（x）可用下式表示： 例如采用0.05J/㎡紫外线照射大肠杆菌时，每个基因组（～4×106核苷酸对）平均产生3个嘧啶二体。实际上每个基因组二体的分布是服从泊松分布的，将取如下形式： …… 是未产生二体的菌的存在概率，实际上其值的5%与采用0.05J/㎡照射时的大肠杆菌uvrA-株，recA-株（除去既不能修复又不能重组修复的二重突变）的生存率是一致的。由于该菌株每个基因组有一个二体就是致死量，因此就意味着全部死亡的概率。 推导

泊松流、指数分布、爱尔朗分布

三种常用的理论分布： （1） 泊松流与泊松分布 ｛N （t ）,t>0｝是计数过程，有 ,2,1,0,! )()(==-n e n t t P t n n λλ 且E[N （t ）]=λt ，Var[N(t)]=λt. (2) 指数分布 当输入过程是一个泊松过程｛N(t),t>0｝时，设T 是两位顾客相继到达的时间间隔，有 F T （t ）=P ｛T ≤t ｝=1－P ｛T ＞t ｝ =1－P 0（t ）=1－t e λ-， t>0, F T （t ）=0, t ≤0。 从 而 ?? ?≤>='=-.0, 00, )()(t t e t F t f t T T λλ（λ＞ 0）， 且 E （T ）=1/λ，

λ—单位时间到达的平均顾客数； 1/λ— 相继到达的平均间隔时间。 定理.输入过程｛N(t), t>0｝是参数为λ的泊松过程的充分必要条件是相继到达的时间间隔：T 1，T 2，…T n ,…相互独立，同服从参数为指数分布。 为一位顾客服务的时间V 一般也服从指数分布，有 ?? ?<>-=-.0,0,0, 1)(t t e t F t V μ, ???<>-=-.0, 0,0, )(t t e t f t V μμ 其中 μ— 平均服务率； E （V ）= 1/μ—一位顾客的平均服务时 间。 ρ=λ/μ—服务强度，刻画服务效率和服务机构利用程度的重要指标。 （3）爱尔朗（Erlang ）分布 设V 1，V 2，…，V k 相互独立，V i ～E(0 ，k μ)，则，T=V 1+V 2+…+V k 的概率密度为

?? ???<>-=-. 0,0, 0,)! 1()()(1t t k kt k t f k k μμ 称T 服从k 阶爱尔朗分布。 例：串列的k 个服务台，每个服务台的服务时间相互独立，服从相同的指数分布，则k 个服务台的总服务时间服从k 阶爱尔朗分布。 有：1）E （T ）=μμ1 1)(1=?=∑=k k V E k i i ； 2）k=1时，T ～E （0，μ）； 3）k ≥30时，T 近似服从正态分布； 4）.01 )(2lim lim ==∞→∞→μk T Var t k （化为确定型分布）。 （注：文档可能无法思考全面，请浏览后下载，供参考。可复制、编制，期待你的好评与关注）