二次函数中有关线段和角度的问题

与线段有关的问题

类型一:已知共线的线段关系-----------------转化为A 字型或8字型

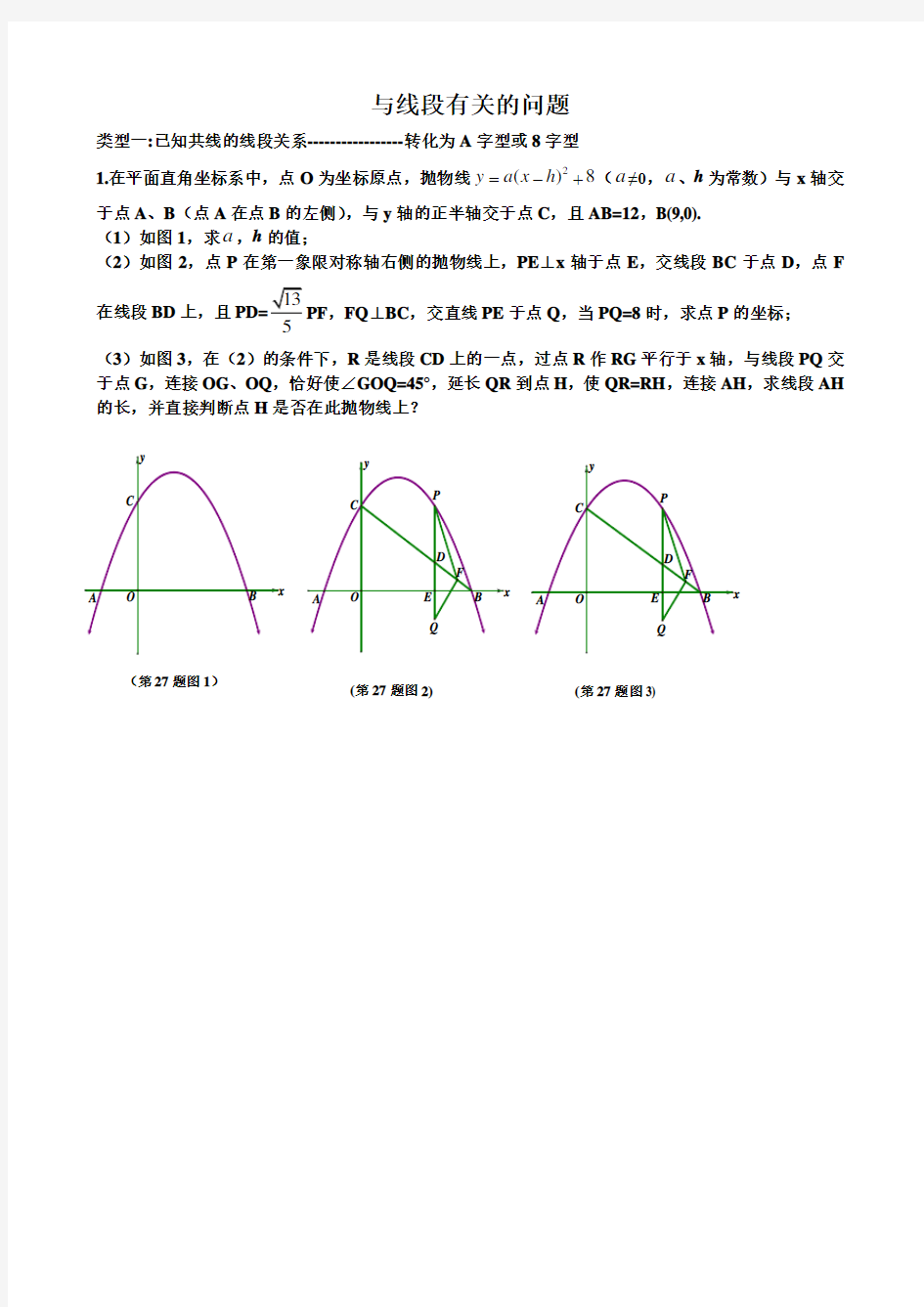
1.在平面直角坐标系中，点O 为坐标原点，抛物线2()8y a x h =-+（a ≠0，a 、h 为常数）与x 轴交于点A 、B （点

A 在点

B 的左侧），与y 轴的正半轴交于点

C ，且AB=12，B(9,0). （1）如图1，求a ，h 的值；

（2）如图2，点P 在第一象限对称轴右侧的抛物线上，PE ⊥x 轴于点E ，交线段BC 于点D ，点F 在线段BD 上，且PF ，FQ ⊥BC ，交直线PE 于点Q ，当PQ=8时，求点P 的坐标； （3）如图3，在（2）的条件下，R 是线段CD 上的一点，过点R 作RG 平行于x 轴，与线段PQ 交于点G ，连接OG 、OQ ，恰好使∠GOQ=45°，延长QR 到点H ，使QR=RH ，连接AH ，求线段AH 的长，并直接判断点H 是否在此抛物线上？

类型二: 已知不共线的两条线段关系---------利用三角函数解决问题

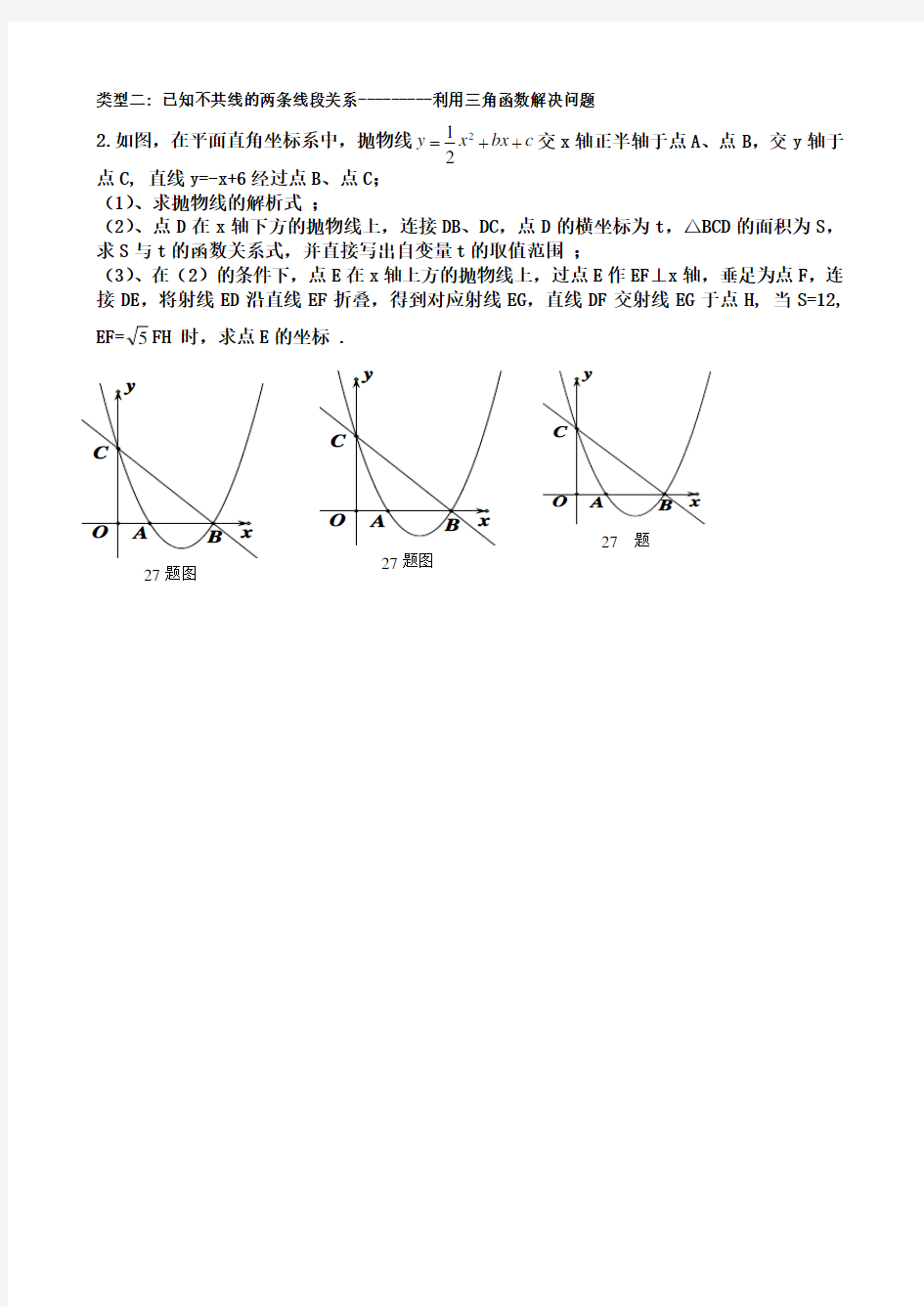
2.如图，在平面直角坐标系中，抛物线2

12

y x bx c =

++交x 轴正半轴于点A 、点B ，交y 轴于点C, 直线y=-x+6经过点B 、点C ； （1）、求抛物线的解析式 ； （2）、点D 在x 轴下方的抛物线上，连接DB 、DC ，点D 的横坐标为t ，△BCD 的面积为S ，求S 与t 的函数关系式，并直接写出自变量t 的取值范围 ； （3）、在（2）的条件下，点E 在x 轴上方的抛物线上，过点E 作EF ⊥x 轴，垂足为点F ，连接DE ，将射线ED 沿直线EF 折叠，得到对应射线EG ，直线DF 交射线EG 于点H, 当S=12, EF=5FH 时，求点E 的坐标 .

类型三:等腰+直角-----------构造中点直角三角形 3.如图，已知抛物线622

12

+--

=x x y 与y 轴交于点A ，与x 轴交于B 、C 两点,连接AC. （1）求直线AC 的解析式；

（2）点P 为直线AC 上方抛物线上的一点，过点P 作PD ⊥AC 点D ，当线段PD 的最长时，求点P 的坐标； （3）在（2）的条件下，连接PB ，Q 为抛物线上一动点，过点Q 做QF ⊥PB 交直线PB 于点F.若Q 点的横坐标为t ，抛物线的对称轴与AC 交于点E ，求t 为何值时,EF=QE?

类型四:利用已知线段构造可解的三角形

4.如图，在平面直角坐标系中，抛物线的顶点A（-1,0）在x轴上，与y轴交于点B，点C（1,4）为抛物线上一点，CD∥x轴交抛物线于点D.

（1）求抛物线的解析式；

（2）点P为抛物线对称轴左侧图象上一动点，设点P的横坐标为t，△PBC的面积为S，求S与t的函数关系式；

（3）在（2）的条件下，延长CP至点Q，使PQ=CP，在线段DB的延长线上取一

点M，使∠DMQ=∠DCB，连接QM交射线CB于点N，当QN=

55

12

时，求t的值.

（第27题图）（第27题备用图）

（第27题备用图）

与角有关的问题

类型一:与已知直线成定角问题

1.如图，已知抛物线32

++=bx ax y （a ≠0）的顶点坐标为Q （2，-1），且与x 轴交于A 、B 两点（点A 在点B 的右侧），连接AC.

（1）求该抛物线的函数关系式

（2）点P 是抛物线上一个动点，从点C 出发沿抛物线向点A 运动，过点C 作射线CD ∥x 轴，交抛物线于点D ，直线PC 交x 轴于点K ，将线段CK 绕点C 逆时针旋转90°得到CK ’，过点K ’作K ’M ∥AC 交射线CD 于点M ，连接MK ，求MK 长.

（3）在（2）的条件下，设点P 的横坐标等于t ，连接MA 、DA ，当t 为何值时，∠MAD 与∠OBC 互余.

类型二:倍角问题(倍角与半角之间的转化)

2.在平面直角坐标系中，O 为坐标原点，抛物线2

23y ax ax =-+与x 轴负半轴交于A,与x 轴的正半轴交于点B,与y 轴的正半轴交于点C,且AB=4. (1) 如图1,求a 的值.

(2) 如图2,连接AC,BC,点D 在第一象限内抛物线上,过D 作DE//AC,交线段BC 于E,若求点D 的坐标.

(3) 如图3,在(2)的条件下,连接DC 并延长,交x 轴于点F,点P 在第一象限的抛物线上,连接PF,作CQ ⊥PF,

交x 轴于Q,连接PQ,当2PQC PFQ ∠=∠时,求点P 的坐标.

类型三:转化为基本图形

3在平面直角坐标系中，点O 为坐标原点，抛物线y=ax2+c 交x 轴于A 、B ，直线y=43x+4

9

过点A ，交y 轴和抛物线分别于D 、C 的横坐标为

2

3

。 （1）求抛物线解析式；

（2）如图2，动点P 在抛物线BC 段上（不与B 、C 重合），连接PA 交OD 于Q ，设线段QD 的长为d ，点P 的横坐标为t ，求d 与t 之间的函数关系式，直接写出t 的取值范围； （3）如图3，在（2）的条件下，直线y=-

2

1

x+k 交OB 、y 轴、AP 、AC 分别于E 、T 、F 、H ，连接PE ，若PE=AH ，且∠APE+∠AHE=180°，求点P 的坐标和DQ 的长。

图1 图2

类型四:2∠A+3∠B=180°---------转化为等腰的问题

4．如图，在平面直角坐标系中，点O 为坐标原点，抛物线1)2(2

--=x a y 与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的顶点为D ，对称轴DE 交x 轴于点E ，OC=3DE ． （1）求a 的值；

（2）如图2，点P 为点B 右侧的抛物线上一点，连接PB 、PA ，直线PB 、PA 分别交对称轴于点Q 、G ，求证:点D 为GQ 的中点；

（3）如图3，点P 为点B 右侧的抛物线上一点，直线PA 交y 轴于点Q ，PF ⊥x 轴于点F ，连接CB ，直线CB 交直线PF 于点K ，点S 在线段PK 上，当SK=2PS ，2∠PQS+3∠QPK=180°时，求点P 的横坐标．

第27题图1

第27题图2 第27题图3

1.二次函数与线段最值

第一讲 二次函数与线段最值 1．如图，已知二次函数223y x x -=-+的图象交x 轴于A 、B 两点（A 在B 左边），交y 轴于C 点． （1）求A 、B 、C 三点的坐标和直线AC 的解析式； （2）点P 是直线AC 上方抛物线上一动点（不与A ，C 重合），过点P 作y 轴平行线交直线AC 于Q 点，求线段PQ 的最大值； （3）点P 是直线AC 上方抛物线上一动点（不与A ，C 重合），过点P 作x 轴平行线交直线AC 于M 点，求线段P M 的最大值； （4）点P 是直线AC 上方抛物线上一动点（不与A ，C 重合），求P 点到直线AC 距离的最大值； （5）点P 是直线AC 上方抛物线上一动点（不与A ，C 重合），连接P A ，PC ，求△P AC 面积的最大值． y x A C O B 竖直线 y x B (x ,y 2) A (x ,y 1) O y x A (x 1,y ) B (x 2,y )O AB =|y 1-y 2|=y 1-y 2 (纵坐标相减)上减下 水平线 AB =|x 1-x 2|=x 2-x 1 (横坐标相减)右减左

2．如图，抛物线223y x x -=-+的图象与x 轴交于A 、B 两点（点A 在点B 左边），与y 轴交于点C ，点D 为抛物线的顶点． （1）求点A 、B 、C 的坐标； （2）点M 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作x 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作PQ ∥AB 交抛物线于点Q ，过点Q 作QN ⊥x 轴于点N ，若点P 在点Q 左边，当矩形PMNQ 的周长最大时，求△AEM 的面积．

二次函数最值问题及解题技巧(个人整理)

一、二次函数线段最值问题 1、平行于x轴的线段最值问题 1）首先表示出线段两个端点的坐标 2）用右侧端点的横坐标减去左侧端点的横坐标 3）得到一个线段长关于自变量的二次函数 4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 2、平行于y轴的线段最值问题 1）首先表示出线段两个端点的坐标 2）用上面端点的纵坐标减去下面端点的纵坐标 3）得到一个线段长关于自变量的二次函数解析式 4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 3、既不平行于x轴，又不平行于y轴的线段最值问题 1）以此线段为斜边构造一个直角三角形，并使此直角三角形的两条直角边分别平行于x轴、y轴 2）根据线段两个端点的坐标表示出直角顶点坐标 3）根据“上减下，右减左”分别表示出两直角边长 4）根据勾股定理表示出斜边的平方（即两直角边的平方和） 5）得到一个斜边的平方关于自变量的二次函数 6）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 7）根据所求得的斜边平方的最值求出斜边的最值即可 二、二次函数周长最值问题 1、矩形周长最值问题 1）一般会给出一点落在抛物线上，从这点向两坐标轴引垂线构成一个矩形，求其周长最值 2）可先设此点坐标，点p到x轴、y轴的距离和再乘以2，即为周长 3）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 2、利用两点之间线段最短求三角形周长最值 1）首先判断图形中那些边是定值，哪些边是变量 2）利用二次函数轴对称性及两点之间线段最短找到两条变化的边，并求其和的最小值3）周长最小值即为两条变化的边的和最小值加上不变的边长 三、二次函数面积最值问题 1、规则图形面积最值问题（这里规则图形指三角形必有一边平行于坐标轴，四边形必有一组对边平行于坐标轴） 1）首先表示出所需的边长及高 2）利用求面积公式表示出面积 3）得到一个面积关于自变量的二次函数 4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 2、不规则图形面积最值问题 1）分割。将已有的不规则图形经过分割后得到几个规则图形 2）再分别表示出分割后的几个规则图形面积，求和 3）得到一个面积关于自变量的二次函数 4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值 或1）利用大减小，不规则图形的面积可由规则的图形面积减去一个或几个规则小图形的面积来得到

二次函数线段最值问题

二次函数线段最值问题 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-

二次函数线段最值问题 ———几何类 “最短距离”经典问题汇总 一、“两点之间线段最短”． 【基本问题】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之和最小，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，与l 的交点即为P 点． 【变式1】直线12l l 、交于O ，P 是两直线间的一点，在直线12l l 、上分别找 一点A B 、，使得PAB ?的周长最短．如图所示，作P 点关于12l l 、的对称点12P P 、，连接12P P ，与12l l 、分别交于A B 、两点，即为所求． 【变式2】直线12l l 、交于O ，A B 、是两直线间的两点，从点A 出发，先到1l 上一点 P ，再从P 点到2l 上一点Q ，再回到B 点，求作P Q 、两点，使AP PQ QB ++最小．如 图所示，作A B 、两点分别关于直线12l l 、的对称点A B 、′′，连接A B ′′ 分别交12l l 、于P Q 、，即为所求． 【变式3】从A 点出发，先到直线l 上的一点P ，再在l 上移动一段固定的距离PQ ， O B A P 2P 1P l 2l 1

再回到点B ，求作P 点使移动的距离最短，如图所示．先将A 点向右平移到A ′点，使AA ′等于PQ 的长，作点B 关于l 的对称点B ′，连接A B ′′，与直线l 的交点即为Q 点，将Q 点向左平移线段PQ 的长，即得到P 点． 【变式4】下面这个题与对称无关，但涉及到了平移的内容，与【变式4】的作法有点类似，因此放在这里，共享一下． A B 、是位于河两岸的两个村庄，要在这条宽度为d 的河上垂直建一座桥，使得从A 村庄经过桥到B 村庄所走的路程最短．如图所示，将点A 向垂直于河岸的方向向下平移距离d ，到A ′点，连接A B ′交河岸于Q 点，过Q 点作PQ 垂直于河岸，交河岸的另一端为P ，即为所求． 【变式5】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之差的绝对值最大，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，其延长线与l 的交点即为P 点． 二、“垂线段最短”． 例题探究： 【探究1】 如图，抛物线42 12+--=x x y 与x 轴的两个交点分别为A （－4，0）、B （2，0），与y 轴交于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ．

二次函数有关线段和差面积最值问题-doc

二次函数之最值问题 ◆ 线段和或差（或三角形周长）最值问题:此类问题一般是利用轴对称的性质和两点之间线段最短确定最 短距离,这个距离一般用勾股定理或两点之间距离公式求解．特殊地，也可以利用平移和轴对称的知识求解固定线段长问题． ◆ 最短距离和找法:以动点所在的直线为对称轴，作一个已知点的对称点，连结另一个已知点和对称点的 线段，与对称轴交于一点,这一点即为所求点.线段长即为最短距离和. ◆ 线段长最值问题：根据两点间距离公式12x x -把线段长用二次函数关系式表示出来求最值. 几何面积最值问题：此类问题一般是先运用三角形相似，对应线段成比例等性质或者用“割补法”或者利用平行线得到三角形同底等高进行面积转化写出图形的面积ｙ与边长x 之间的二次函数关系,其顶点的纵坐 标即为面积最值． 例１、已知二次函数2y x bx c =++的图象过点()3,0A -和点()1,0B ，且与y 轴交于点C ，D 点在抛物线上且横坐标是2-．(1)求抛物线的解析式;(２)抛物线的对称轴上有一动点P,求出PA PD +的最小值．? ? ?例2、如图，在平面直角坐标系xOy 中,直线3 2y x =- +分别交ｘ轴、y 轴于C 、A 两点.将射线AM 绕着点Ａ顺时针旋转4５°得到射线AN.点D 为ＡＭ上的动点，点B 为AN 上的动点，点C 在∠MAN 的内部. （1)求线段A Ｃ的长； (２）求△BC Ｄ周长的最小值； （3)当△BCD 的周长取得最小值,且52 BD =时,△BCD 的面积为＿＿__＿___. ? ?????1、已知抛物线21y ax bx =++经过点()1,3A 和点()2,1B ．（１）求此抛物线解析式； (２)点Ｃ、D 分别是ｘ轴和y 轴上的动点,求四边形ABCD 周长的最小值;?(3)过点Ｂ作x 轴的垂线,垂足为E 点．点P 从抛物线的顶点出发,先沿抛物线的对称轴到达F 点，再沿FE 到达E 点，若P 点在对称轴上的运动速度是它在直线FE 上运动速度的2倍，试确定点F 的位置,使 得点P 按照上述要求到达E 点所用的时间最短．????

二次函数线段、周长、面积最值问题

二次函数线段、周长、面积最值问题 1．如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C 点坐标是（4，3）． （1）求抛物线的解析式； （2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标． （变式）如图，已知抛物线y=ax2+bx+c经过A（-3，0），B（1，0），C（0，3）三点，其顶点为D，对称轴是直线l，l与x 轴交于点H． （1）求该抛物线的解析式； （2）若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值； （3）如图（2），若E是线段AD上的一个动点（ E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S． ①求S与m的函数关系式； ②S是否存在最大值？若存在，求出最大值及此时点E的坐标；若不存在，请说明理由．

2．已知：抛物线l1：y=-x2+bx+3交x轴于点A，B，（点A在点B的左侧），交y轴于点C，其对称轴为x=1，抛物线l2经过点A，与x轴的另一个交点为E（5，0），交y轴于点D（0，- 5/2）． （1）求抛物线l2的函数表达式； （2）P为直线x=1上一动点，连接PA，PC，当PA=PC时，求点P的坐标； （3）M为抛物线l2上一动点，过点M作直线MN∥y轴，交抛物线l1于点N，求点M自点A运动至点E的过程中，线段MN长度的最大值．

二次函数线段最值问题

次函数线段最值问题 —几何类 “最短距离”经典问题汇总 一、 “两点之间线段最短”. 【基本问题】在直线I 上找一点P ，使得其到直线异侧两点A 、B 的距离之和最小，如图所示?作点 A （或B ）关于直线I 的对称点，再连接另一点与对称点，与I 的交点即为P 点. 【变式1】直线爪I 2交于O ，P 是两直线间的一点，在直线11、12上分别找一点 A 、B ，使得PAB 的周长最短?如图所示，作P 点关于h 、J 的对称点P 、P 2，连 接PP ，与h 、J 分别交于A 、B 两点，即为所求. 【变式2】直线l i 、I 2交于O ，A 、B 是两直线间的两点，从点A 出发，先到I i 上 一点P ，再从P 点到I 2上一点Q ，再回至U B 点，求作P 、Q 两点，使AP PQ QB 最小?如图所示，作A 、B 两点分别关于直线h 、I 2的对称点A 、B ：连接AB 分 别交I i 、12于P 、Q ，即为所求. 【变式3】从A 点出发，先到直线I 上的一点P ，再在I 上移动一段固定的距离PQ ，再回到点B ， 求作P 点使移动的距离最短， 轴交于点C,顶点为D. E （1, 2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别 交于F 、G. 在直线EF 上求一点H ,使A CDH 的周长最小，并求出最小周长； 【探究2】已知在平面直角坐标xOy 系抛物线y x 2 2x 3与x 轴交于 A 、 B 两点（点A 在点B 的左侧），与y 轴交于点 C 。若一个动点 P 自点C 出发，先到达x 轴上某点（设为点E ），再到达抛物线 的对称轴上某点（设为点F ），最后运动到点C .求使点P 运动 的总路径最短的点E 、点F 的坐标，并求出这个最短总路径的长. 【探究3】 已知在平面直角坐标xOy 系抛物线y x 2 2x 3与x 轴 交于A B 两点（点A 在点B 的左侧），与y 轴交于点C ,在 线段 BC 上是否存在一点P ，使得B 、C 两点到直线AP 的距 离之和最 大？若存在，请求出P 点的坐标；若不存在，请说 明理由。 【探究4】已知在平面直角坐标xOy 系抛物线y x 2 2x 3与x 轴交于A B 两点 （点A 在点B 的左 侧），与y 轴交于点C 。若一个动点P 自OC 的中点M 出发，先到达x 轴上某点（设为点E ）， 再到达抛物线 的对称轴上某点（设为点 F ），最后运动到点C .求使点P 运动 的总路径最 短的点E 、点F 的坐标，并求出这个最短总路径的 如图所示?先将A 点向右平移到A ，点，使AA 等于PQ 的长，作点B 关 于I 的对称点B ，,连接AB ,与直线I 的交点即为Q 点，将Q 点向左平移线段PQ 的长，即得到P 点. 【变式4】下面这个题与对称无关，但涉及到了平移的内容，与【变式 4】的作 法有点类似，因此放在这里，共享一下. A 、 B 是位于河两岸的两个村庄，要在这条宽度为d 的河上垂直建一座桥，使得从 A 村庄经过桥到B 村庄 所走的路程最短.如图所示，将点 A 向垂直于河岸的方向 向下平移距离d ，到A ，点，连接AB 交河岸于Q 点，过Q 点作PQ 垂直于河岸，交 河岸的另一端为P ，即为所求. 【变式5】在直线I 上找一点P ，使得其到直线异侧两点 A 、B 的距离之差的绝对 值最大，如图所示.作点A 交点即为P 点. 二、 “垂线段最短”. 例题探究： 【探究1】 如图，抛物线y （或B ） 关于直线I 的对称点，再连接另一点与对称点, 'P A' d Q 卄 B 其延长线与I 的 x 4与x 轴的两个交点分别为 A （-4, 0）、B （2, 0），与y 2 F O B x

二次函数中线段最值问题

二次函数中线段最值问题（一） 例1.已知，抛物线y＝ax2+bx+c，过A（﹣1，0）、B（3，0）、C（0，﹣3），M为顶点．（1）求抛物线的解析式；y＝x2﹣2x﹣3 （2）在该抛物线的对称轴上找一点P，使得PA+PC的值最小，并求出P的坐标； 练习1.如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，抛物线y＝﹣x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D． （1）求抛物线的解析式；y＝﹣x2+2x+3， （2）在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值； 练习2.如图，抛物线y＝x2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．（1）求抛物线的解析式及顶点D的坐标；y＝x2﹣2x﹣3， （2）点M是对称轴上的一个动点，当△ACM的周长最小时，求点M的坐标．

例2.如图，已知抛物线y＝ax2+bx+3（a≠0）经过点A（1，0）和点B（3，0），与y轴交于点C．（1）求此抛物线的解析式；y＝x2﹣4x+3 （2）若点T为对称轴直线x＝2上一点，则TC﹣TB的最大值为． 练习3.在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y＝x2﹣x﹣2的顶点为D，交x轴于点A、B（点A在点B左侧），交y 轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P． （1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；y＝＝2x2﹣6x﹣8．（2）当BP﹣CP的值最大时，求点P的坐标； 例3.如图，抛物线y＝ax2+bx+2与x轴交于A，B两点，且OA＝2OB，与y轴交于点C，连 接BC，抛物线对称轴为直线x＝，D为第一象限内抛物线上一动点，过点D作DE⊥ OA于点E，与AC交于点F，设点D的横坐标为m． （1）求抛物线的表达式；y＝﹣x2+x+2； （2）当线段DF的长度最大时，求D点的坐标；

天津市2018年中考数学题型专项训练二次函数与线段问题含答案

二次函数与线段问题 1.已知抛物线经过点A (－1,0)、B (3,0)、C (0,－3). (Ⅰ)求抛物线的解析式及其顶点D 的坐标; (Ⅱ)直线CD 交x 轴于点E ,过抛物线上在对称轴右边的点P ,作y 轴的 平行线交x 轴于点F ,交直线CD 于点M ,使PM =2 5EF ,请求出点P 的坐 标; (Ⅲ)将抛物线沿对称轴平移,要使抛物线与(Ⅱ)中的线段EM 总有交点,那么抛物线向上最多平移多少个单位长度?向下最多平移多少个单位长度? 解:(Ⅰ)设抛物线解析式为y =a (x ＋1)(x －3), 把点C (0,－3)代入得:a ×1×(－3)=－3, 解得a =1, ∴抛物线解析式为y =(x ＋1)(x －3), 即y =x 2－2x －3, ∵y =x 2－2x －3=(x －1)2－4, ∴顶点D 的坐标为(1,－4); (Ⅱ)如解图,设直线CD 的解析式为y =kx ＋b , 把点C (0,－3),D (1,－4)代入得 34b k b =-??+=-?,解得13k b =?? =?－ －, ∴直线CD 的解析式为y =－x －3,

当y=0时,－x－3=0, 解得x=－3, 则E(－3,0), 设P(t,t2－2t－3)(t＞1), 则M(t,－t－3),F(t,0), ∴EF=t＋3,PM=t2－2t－3－(－t－3)=t2－t, 而PM=2 5 EF, ∴t2－t=2 5 (t＋3), 整理得5t2－7t－6=0, 解得t1=－3 5 (舍去),t2=2, 当t=2时,t2－2t－3=22－2×2－3=－3, ∴点P坐标为(2,－3); 第1题解图 (Ⅲ)当t=2时,点M的坐标为(2,－5), 设平移后的抛物线解析式为y=x2－2x－3＋m, 当抛物线y=x2－2x－3＋m与直线y=－x－3有唯一公共点时,

二次函数线段最值问题

二次函数线段最值问题 ———几何类 “最短距离”经典问题汇总 一、“两点之间线段最短”． 【基本问题】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之和最小，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，与l 的交点即为P 点． 【变式1】直线12l l 、交于O ，P 是两直线间的一点，在直线12l l 、上分别找 一点A B 、，使得PAB ?的周长最短．如图所示，作P 点关于12l l 、的对称点12P P 、，连接 12P P ，与12l l 、分别交于A B 、两点，即为所求． 【变式2】直线12l l 、交于O ，A B 、是两直线间的两点，从点A 出发，先到1l 上一点P ，再从P 点到2l 上一点Q ，再回到B 点，求作P Q 、两点，使AP PQ QB ++最小．如图所示，作A B 、两点分别关于直线12l l 、的对称点A B 、′′，连接A B ′′分别交12l l 、于P Q 、，即为所求． 【变式3】从A 点出发，先到直线l 上的一点P ，再在l 上移动一段固定的距离PQ ，再回到点B ，求作P 点使移动的距离最短，如图所示．先将A 点向右平移 到A ′点，使AA ′等于PQ 的长，作点B 关于l 的对称点B ′，连接A B ′′ ，与直线O B A P 2P 1P l 2l 1

l 的交点即为Q 点，将Q 点向左平移线段PQ 的长，即得到P 点． 【变式4】下面这个题与对称无关，但涉及到了平移的内容，与【变式4】的作法有点类似，因此放在这里，共享一下． A B 、是位于河两岸的两个村庄， 要在这条宽度为d 的河上垂直建一座桥，使得从A 村庄经过桥到B 村庄所走的路程最短．如图所示，将点A 向垂直于河岸的方向向下平移距离d ，到A ′点，连接A B ′交河岸于Q 点，过Q 点作PQ 垂直于河岸，交河岸的另一端为P ，即为所求． 【变式5】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之差的绝对值最大，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，其延长线与l 的交点即为P 点． 二、“垂线段最短”． 例题探究： 【探究1】 如图，抛物线42 12+--=x x y 与x 轴的两个交点分别为A （－4，0）、B （2， 0），与y 轴交于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ． 在直线EF 上求一点H ，使△CDH 的周长最小，并求出最小周 长；

二次函数中线段和差最值问题

二次函数中线段和、差最值问题 姓名： 1、如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；并求出周长的最小值；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．

2、如图，△ABC的三个顶点坐标分别为A（-2，0）、B（6，0）、C（0，3 2 -），抛物线y=ax2+bx+c （a≠0）经过A、B、C三点。（1）求直线AC的解析式；（2）求抛物线的解析式；（3）若抛物线的顶点为D，在直线AC上是否存一点P，使得△BDP的周长最小，若存在，求出P点的坐标；若不存在，请说明理由。 3、如图，已知直线 1 1 2 y x =+与y轴交于点A，与x轴交于点D，抛物线2 1 2 y x bx c =++与直 线交于A、E两点，与x轴交于B、C两点，且B点坐标为(1，0)。⑴求该抛物线的解析式； ⑵动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标P。⑶在抛物线的对称轴上找一点M，使|| AM MC -的值最大，求出点M的坐标。

4、如图8，对称轴为直线x =2的抛物线经过点A （-1，0），C （0，5）两点，与x 轴另一交点为B ，已知M （0，1），E （a ，0），F （a +1，0），点P 是第一象限内的抛物线上的动点．（1）求此抛物线的解析式．（2）当a =1时，求四边形MEFP 面积的最大值，并求此时点P 的坐标．（3）若△PCM 是以点P 为顶点的等腰三角形，求a 为何值时，四边形PMEF 周长最小？请说明理由． 图8 O A E F B M C P x y 备用图 A O M C E F x B y P

二次函数的线段最值问题

二次函数的线段最值问题

————————————————————————————————作者：————————————————————————————————日期：

例１:如图，抛物线经过了点Ａ(4，0），B(-4，-4）,C(０,2)，连接AB,ＢC,ＡC, （１）求抛物线解析式。 (2）点P是抛物线对称轴上的一点,求△ＰBC周长的最小值及此时P点的坐标。 2．已知如图，抛物线y=x2+bx+ｃ过点Ａ（3,0）,B(1,0），交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动（点P不与点A重合）,过点P 作PD∥y轴交直线ＡＣ于点D． (1)求抛物线的解析式; （2）求点Ｐ在运动的过程中线段PＤ长度的最大值; (3)在抛物线对称轴上是否存在点M使|MＡ﹣MＣ｜最大？若存在请求出点Ｍ的坐标，若不存在请说明理由. y F O B C A D E

3.如图，抛物线21442 y x x =-+与y 轴交于点Ａ,B 是ＯＡ的中点.一个动点G 从点B 出发,先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点Ａ.如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程． ４.如图，菱形ＡB ＣD 的边长为6且∠DAB=60°,以点A 为原点、边AB 所在的直线为x 轴且顶点D 在第一象限建立平面直角坐标系.动点P 从点D 出发沿折线D ＣB 向终点B 以2单位/每秒的速度运动，同时动点Q 从点Ａ出发沿ｘ轴负半轴以1单位/秒的速度运动，当点Ｐ到达终点时停止运动,运动时间为t,直线PQ 交边AD 于点E ． （1)求出经过Ａ、D 、C 三点的抛物线解析式； （2）若F 、G 为ＤC 边上两点，且点ＤＦ=ＦＧ=１，试在对角线D Ｂ上找一点M 、抛物线ＡDC 对称轴上找一点N,使得四边形FMNG 周长最小并求出周长最小值．

2018年秋季压轴题班第二讲(二次函数中的定值问题、线段角度问题)

第二讲二次函数中的定值问题、线段角度问题 知识纵横 如何破解二次函数 破解压轴题，是个系统工程，不是一蹴而就的，需要一个积累和磨砺的过程。 你要有广博的知识根基，要有强大的运算能力，还必须掌握一定的数学思想方法和解题技巧，数学思想方法不是光记住两个名称，而是要掌握其本质核心的东西。比如转化思想，转化谁？怎么转化？没有谁告诉你，你得自己完成；再如分类讨论思想，在什么情况下分类讨论，分类的标准是什么？为什么要这样分而不是那样分呢？有时候还涉及二次分类，即分类之后再分类，你看得出吗？你要会画草图，能从繁杂的信息里面提取有效的信息，能从复杂的图形里面抽出基本图形，能准备理解语句的含义建立问题模型，形成简洁思路，并规范正确地表述解题过程。 类型三定值问题 2 2 例一：如图，直线y =x?1与抛物线y = x -2mx m - m交于A,B两点（点A在点B的左边）。求证: 无论m为何值，AB的长总为定值。

变式一如图，已知直线y二kx-9k kvO与抛物线_2x_3交于A,B两点，与x轴交于点P,过点A作AC丄x轴于点C,过点B作BD± x于点D,求证：PD PC为定值。 变式二如图，抛物线y=x2-4x?3与x轴交于A,B两点，与y轴交于点C,将直线BC沿y轴向上平移交抛物线于点M,N,交y轴于点P,求PM -PN的值。 例二：（2016-天河一模）如图，抛物线的顶点坐标为C（ 0,8 ）,并且经过A（ 8,0 ）,点P是抛物线上点A,C 间的

一个动点（含端点），过点P作直线y =8的垂线，垂足为点F,点D, E的坐标分别为（0,6），（4,0），连接PD,PE,DE （1）求抛物线的解析式； （2）猜想并探究：对于任意一点P，PD与PF的差是否为固定值，如果是，请求出此定值，如果不是，请说明理 由； （3）求：①当三角形PDE的周长最小时的点P坐标；②使三角形PDE的面积为整数的点P的个数。 3『SJ

中考数学中的二次函数的线段和差以最值问题

二次函数与线段和差问题 例题精讲：如图抛物线与x轴交于A,B（1,0），与y 轴交于点C,直线经过点A,C.抛物线的顶点为D，对称轴为直线l, （1）求抛物线解析式。 （2）求顶点D的坐标与对称轴l. （3）设点E为x轴上一点，且AE=CE,求点E的坐标。 （4）设点G是y轴上的一点，是否存在点G，使得GD+GB的值最小，若存在，求出G点坐标，若不存在，说明理由。 （5）在直线l上是否存在一点F，使得△BCF的周长最小，若存在，求出点F 的坐标及△BCF周长的最小值，若不存在，说明理由。 （6）在y轴上是否存在一点S,使得SD-SB的值最大，若存在，求出S点坐标，若不存在，说明理由。 （7）若点H是抛物线上位于AC上方的一点，过点H作y轴的平行线，交AC 于点K，设点H的横坐标为h,线段HK=d ①求d关于h的函数关系式 ②求d的最大值及此时H点的坐标 （8）设点P是直线AC上方抛物线上一点，当P点与直线AC距离最大值时，求P点的坐标，并求出最大距离是多少？

1.如图，矩形的边OA在轴上，边OC在轴上，点的坐标为(10,8)，沿直线OD折叠矩形，使点正好落在上的处，E点坐标为(6,8)，抛物线经过、、三点。（1）求此抛物线的解析式。 （2）求AD的长。 （3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标。

2.如图，在平面直角坐标系 中，抛物线4 1 2+ =x y 与轴相交于点A ，点B 与点O 关于点A 对称。 （1）填空：点B 的坐标是 。 （2）过点的直线 （其中）与轴相交于 点C ，过点C 作直线平行于轴，P 是直线上一点，且PB=PC ，求线段PB 的长（用含k 的式子表示），并判断点P 是否在抛物线上，说明理由。 （3）在（2）的条件下，若点C 关于直线BP 的对称点恰好落在该抛物线的对称轴上，求此时点P 的坐标。

二次函数与线段问题(解析版)

二次函数与线段问题 例1、 如图1-1，抛物线y ＝x 2－2x －3与x 轴交于A 、B 两点，与y 轴交于点C ，点P 是抛物线对称轴上的一个动点，如果△P AC 的周长最小，求点P 的坐标． 图1-1 【解析】如图1-2，把抛物线的对称轴当作河流，点A 与点B 对称，连结BC ，那么在△PBC 中，PB ＋PC 总是大于BC 的．如图1-3，当点P 落在BC 上时，PB ＋PC 最小，因此P A ＋PC 最小，△P AC 的周长也最小． 由y ＝x 2－2x －3，可知OB ＝OC ＝3，OD ＝1．所以DB ＝DP ＝2，因此P (1,－2)． 图1-2 图1-3 例2、如图，抛物线21442 y x x =-+与y 轴交于点A ，B 是OA 的中点．一个动点G 从点B 出发，先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点A ．如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程． 图2-1 【解析】如图2-2，按照“台球两次碰壁”的模型，作点A 关于抛物线的对称轴对称的点A ′，作点B 关于x 轴对称的点B ′，连结A ′B ′与x 轴交于点M ，与抛物线的对称轴交于点N ． 在Rt △AA ′B ′中，AA ′＝8，AB ′＝6，所以A ′B ′＝10，即点G 走过的最短路程为10．根据

相似比可以计算得到OM ＝83，MH ＝43，NH ＝1．所以M (83 , 0)，N (4, 1)． 图2-2 例3、如图3-1，抛物线248293 y x x =-++与y 轴交于点A ，顶点为B ．点P 是x 轴上的一个动点，求线段P A 与PB 中较长的线段减去较短的线段的差的最小值与最大值，并求出相应的点P 的坐标． 图3-1 【解析】题目读起来像绕口令，其实就是求|P A －PB |的最小值与最大值． 由抛物线的解析式可以得到A (0, 2)，B (3, 6)．设P (x , 0)． 绝对值|P A －PB |的最小值当然是0了，此时P A ＝PB ，点P 在AB 的垂直平分线上（如图3-2）．解方程x 2＋22＝(x －3)2＋62，得416x =．此时P 41(,0)6 ． 在△P AB 中，根据两边之差小于第三边，那么|P A －PB |总是小于AB 了．如图3-3，当 点P 在BA 的延长线上时，|P A －PB |取得最大值，最大值AB ＝5．此时P 3(,0)2 -． 图3-2 图3-3 例4、如图4-1，菱形ABCD 中，AB ＝2，∠A ＝120°，点P 、Q 、K 分别为线段BC 、CD 、BD 上的任意一点，求PK ＋QK 的最小值．

二次函数线段最值问题_3

二次函数线段最值问题 ———几何类 “最短距离”经典问题汇总 一、“两点之间线段最短”． 【基本问题】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之和最小，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，与l 的交点即为P 点． 【变式1】直线12l l 、交于O ，P 是两直线间的一点，在直线12l l 、上分别找一点A B 、，使 得PAB ?的周长最短．如图所示，作P 点关于12l l 、的对称点12P P 、，连接12P P ，与12l l 、分 别交于A B 、两点，即为所求． 【变式2】直线12l l 、交于O ，A B 、是两直线间的两点，从点A 出发，先到1l 上一点P ，再从P 点到2l 上一点Q ，再回到B 点，求作P Q 、两点，使AP PQ QB ++最小．如图所示，作A B 、两点分别关于直线12l l 、的对称点A B 、′′，连接A B ′′ 分别交12l l 、于P Q 、，即为所求． 【变式3】从A 点出发，先到直线l 上的一点P ，再在l 上移动一段固定的距离PQ ，再回到点B ，求作P 点使移动的距离最短，如图所示．先将A 点向右平移到A ′点，使AA ′等于PQ 的长，作点B 关于l 的对称点B ′，连接A B ′′，与直线l 的交点即为Q 点向左平移线段PQ 的长，即得到P 点． 【变式4】下面这个题与对称无关，但涉及到了平移的内容，与【变式4因此放在这里，共享一下． A B 、是位于河两岸的两个村庄，要在这条宽度为d 的河上垂直建一座桥，使得从A 过桥到B 村庄所走的路程最短．如图所示，将点A A ′点，连接A B ′交河岸于Q 点，过Q 点作PQ 垂直于河岸，交河岸的另一端为P ， 【变式5】在直线l 上找一点P ，使得其到直线异侧两点A B 、的距离之差的绝对值最大，如图所示．作点A （或B ）关于直线l 的对称点，再连接另一点与对称点，其延长线与l 的交点即为P 点． 二、“垂线段最短”． AB ≥AM+BN N B M A 斜边大于直角边 C B A 垂线段最短 例题探究： 【探究1】 如图，抛物线42 1 2+--=x x y 与x 轴的两个交点分别为A （－4，0）、B （2，0），与y 轴交 于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ． 在直线EF 上求一点H ，使△CDH 的周长最小，并求出最小周长； l A' B P A l O B A P 2 P 1P l 2 l 1 P B'A l

中考复习二次函数综合复习之线段问题(难)(教师版)

二次函数综合复习之线段问题 如图1，在平面直角坐标系xoy 中，抛物线M ：52 12 +-=x y 经过点C(2，3)，直线y ＝kx ＋b 与抛物线相交于A ，B 两点，∠ACB ＝ 90°。 （1）探究与猜想： ①探究：取点B （6，一13）时，点A 的坐标为（一 25，8 15 ），直接写出直线AB 的解析式： ； 取点B （4，－3），直接写出AB 的解析式为________________； ②猜想：我们猜想直线AB 必经过一个定点Q ，其坐标为___________________。请取点B 的横坐标为n ，验证你的猜想； （2）如图2，点D 在抛物线M 上，若AB 经过原点O ，△ABD 的面积等于△ABC 的面积，试求出一个符合条件的点D 的坐标，并直接写出其余的符合条件的D 点的坐标。 （图1） （图2） 【例题精讲一】 二次函数代几综合之线段长度问题 例题 1、（2017江岸模三）已知抛物线2y x ＝上有两动点A ()11x y ，、B ()22x y ，（其中120x x ＜＜），过点A 作AC ⊥x 轴于点C ，过点B 作BC ⊥x 轴于点D ，OA 的延长线交BD 于点E 。 （1）如图1，若点A 的坐标为（1，1），点B 的坐标为（2，4），则点E 的坐标为 ； （2）如图2，过A 作AF ⊥BD 于F 。若BE ＝AE ，试求BF 的长。 （3）如图3，延长CA 交OB 于点H 。若13 OEH OHED S S △四边形＝，试探究12x x 与之间的数量关系，并证明你的结论。

2、（江汉模一）已知抛物线y ＝x 2的图象如图1，A (0，a )（a ＞0），直线l ：4 1 -=y ，点B 为抛物线上的任意一点且恒满足点B 到点A 的距离与点B 到l 的距离相等。 （1）求a 的值； （2）若直线l 1：y ＝kx ＋ 4 1 交抛物线于C 、D 两点，过点C 作CE ⊥l 于点E ，过点D 作DF ⊥l 于点F ，点G 为EF 的中点。若点G 到直线l 1的距离为2 5 ，求k 的值；

二次函数的线段最值问题

例1:如图，抛物线经过了点A（4,0），B（-4，-4），C（0,2），连接AB,BC,AC, （1）求抛物线解析式。 （2）点P是抛物线对称轴上的一点，求△PBC周长的最小值及此时P点的坐标。 过点A（3，0），B（1，0），交y轴于点C，点P A点运动（点P不与点A重合），过点P作PD∥y轴交直线AC于点D． （1）求抛物线的解析式； （2）求点P在运动的过程中线段PD长度的最大值； （3）在抛物线对称轴上是否存在点M使|MA﹣MC|最大？若存在请求出点M的坐标，若不存在请说明理由． y F O B C A D E

3.如图，抛物线21442 y x x =-+与y 轴交于点A ，B 是OA 的中点．一个动点G 从点B 出发，先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点A ．如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程． 4．如图，菱形ABCD 的边长为6且∠DAB=60°，以点A 为原点、边AB 所在的直线为x 轴且顶点D 在第一象限建立平面直角坐标系．动点P 从点D 出发沿折线DCB 向终点B 以2单位/每秒的速度运动，同时动点Q 从点A 出发沿x 轴负半轴以1单位/秒的速度运动，当点P 到达终点时停止运动，运动时间为t ，直线PQ 交边AD 于点E ． （1）求出经过A 、D 、C 三点的抛物线解析式； （2）若F 、G 为DC 边上两点，且点DF=FG=1，试在对角线DB 上找一点M 、抛物线ADC 对称轴上找一点N ，使得四边形FMNG 周长最小并求出周长最小值．

5．如图，抛物线y=﹣x2+bx+c与x轴交于A，B两点，与y轴交于点C，点O 为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3． （1）写出抛物线对应的函数解析式：； （2）连结CB交EF于M，再连结AM交OC于R，求△ACR的周长． （3）设G（4，﹣5）在该抛物线上，P是y轴上一动点，过点P作PH垂直于直线EF并交于H，连接AP，GH，问AP+PH+HG是否有最小值？如果有，求点P 的坐标；如果没有，请说明理由． 6.如图7-1，△ABC中，∠ACB＝90°，AC＝2，BC＝1．点A、C分别在x

二次函数中有关线段和角度的问题

与线段有关的问题 类型一:已知共线的线段关系-----------------转化为A 字型或8字型 1.在平面直角坐标系中，点O 为坐标原点，抛物线2()8y a x h =-+（a ≠0，a 、h 为常数）与x 轴交于点A 、 B （点A 在点B 的左侧），与y 轴的正半轴交于点 C ，且AB=12，B(9,0). （1）如图1，求a ，h 的值； （2）如图2，点P 在第一象限对称轴右侧的抛物线上，PE⊥x 轴于点E ，交线段BC 于点D ，点F 在线段BD 上，且PF ，FQ⊥BC，交直线PE 于点Q ，当PQ=8时，求点P 的坐标； （3）如图3，在（2）的条件下，R 是线段CD 上的一点，过点R 作RG 平行于x 轴，与线段PQ 交于点G ，连接OG 、OQ ，恰好使∠GOQ=45°，延长QR 到点H ，使QR=RH ，连接AH ，求线段AH 的长，并直接判断点H 是否在此抛物线上？

类型二: 已知不共线的两条线段关系---------利用三角函数解决问题 2.如图，在平面直角坐标系中，抛物线2 12 y x bx c = ++交x 轴正半轴于点A 、点B ，交y 轴于点C, 直线y=-x+6经过点B 、点C ； （1）、求抛物线的解析式 ； （2）、点D 在x 轴下方的抛物线上，连接DB 、DC ，点D 的横坐标为t ，△BCD 的面积为S ，求S 与t 的函数关系式，并直接写出自变量t 的取值范围 ； （3）、在（2）的条件下，点E 在x 轴上方的抛物线上，过点E 作EF ⊥x 轴，垂足为点F ，连接DE ，将射线ED 沿直线EF 折叠，得到对应射线EG ，直线DF 交射线EG 于点H, 当S=12, EF=5FH 时，求点E 的坐标 .

(完整版)二次函数的线段最值问题

例1:如图，抛物线经过了点A （4,0），B （-4，-4），C （0,2），连接AB,BC,AC, （1）求抛物线解析式。 （2）点P 是抛物线对称轴上的一点，求△PBC 周长的最小值及此时P 点的坐标。 A （3，0）， B （1，0），交y 轴于点 C ，点P A 点运动（点P 不与点A 重合），过点P 作P D ∥y 轴交直线AC 于点D ． （1）求抛物线的解析式； （2）求点P 在运动的过程中线段PD 长度的最大值； （3）在抛物线对称轴上是否存在点M 使|MA ﹣MC |最大？若存在请求出点M 的坐标，若不存在请说明理由． y F O B C A D E

3.如图，抛物线21442 y x x =-+与y 轴交于点A ，B 是OA 的中点．一个动点G 从点B 出发，先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点A ．如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程． 4．如图，菱形ABCD 的边长为6且∠DAB=60°，以点A 为原点、边AB 所在的直线为x 轴且顶点D 在第一象限建立平面直角坐标系．动点P 从点D 出发沿折线DCB 向终点B 以2单位/每秒的速度运动，同时动点Q 从点A 出发沿x 轴负半轴以1单位/秒的速度运动，当点P 到达终点时停止运动，运动时间为t ，直线PQ 交边AD 于点E ． （1）求出经过A 、D 、C 三点的抛物线解析式； （2）若F 、G 为DC 边上两点，且点DF=FG=1，试在对角线DB 上找一点M 、抛物线ADC 对称轴上找一点N ，使得四边形FMNG 周长最小并求出周长最小值．

二次函数 线段和差最值的存在性问题解题策略

中考数学压轴题解题策略（8） 线段和差最值的存在性问题解题策略 专题攻略 两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）． 三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）． 两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，P A 与PB 的差的最大值就是AB ，此时点P 在AB 的延长线上，即P ′． 解决线段和差的最值问题，有时候求函数的最值更方便，本讲不涉及函数最值问题． 图1 图2 图3 例题解析 例? 如图1-1，抛物线y ＝x 2－2x －3与x 轴交于A 、B 两点，与y 轴交于点C ，点P 是抛物线对称轴上的一个动点，如果△P AC 的周长最小，求点P 的坐标． 图1-1 【解析】如图1-2，把抛物线的对称轴当作河流，点A 与点B 对称，连结BC ，那么在△PBC 中，PB ＋PC 总是大于BC 的．如图1-3，当点P 落在BC 上时，PB ＋PC 最小，因此P A ＋PC 最小，△P AC 的周长也最小． 由y ＝x 2－2x －3，可知OB ＝OC ＝3，OD ＝1．所以DB ＝DP ＝2，因此P (1,－2)． 图1-2 图1-3 例?如图，抛物线21442 y x x =-+与y 轴交于点A ，B 是OA 的中点．一个动点G 从

点B 出发，先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点A ．如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程． 图2-1 【解析】如图2-2，按照“台球两次碰壁”的模型，作点A 关于抛物线的对称轴对称的点A ′，作点B 关于x 轴对称的点B ′，连结A ′B ′与x 轴交于点M ，与抛物线的对称轴交于点N ． 在Rt △AA ′B ′中，AA ′＝8，AB ′＝6，所以A ′B ′＝10，即点G 走过的最短路程为10．根据 相似比可以计算得到OM ＝83，MH ＝43，NH ＝1．所以M (83 , 0)，N (4, 1)． 图2-2 例? 如图3-1，抛物线248293 y x x =-++与y 轴交于点A ，顶点为B ．点P 是x 轴上的一个动点，求线段P A 与PB 中较长的线段减去较短的线段的差的最小值与最大值，并求出相应的点P 的坐标． 图3-1 【解析】题目读起来像绕口令，其实就是求|P A －PB |的最小值与最大值． 由抛物线的解析式可以得到A (0, 2)，B (3, 6)．设P (x , 0)． 绝对值|P A －PB |的最小值当然是0了，此时P A ＝PB ，点P 在AB 的垂直平分线上（如 图3-2）．解方程x 2＋22＝(x －3)2＋62，得416x = ．此时P 41(,0)6 ． 在△P AB 中，根据两边之差小于第三边，那么|P A －PB |总是小于AB 了．如图3-3，当点 P 在BA 的延长线上时，|P A －PB |取得最大值，最大值AB ＝5．此时P 3(,0)2-．